VECTOR-BASE AMPLITUDE PANNING LIBRARY

EXAMPLE 1: Triangulation
EXAMPLE 2: VBAP Gains
EXAMPLE 3: Spreading by amplitude panning
EXAMPLE 4: Gain Tables
EXAMPLE 5: Moving source
EXAMPLE 6: VBAP filters with frequency-dependent P-value
REFERENCES

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
%   Archontis Politis, 2015
%   Department of Signal Processing and Acoustics, Aalto University, Finland
%   archontis.politis@aalto.fi
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

This is a compact Matlab/Octave library implementing vector-base amplitude panning (VBAP) [ref.1], VBAP-base spreading of a panned source [ref.2&3], and Multiple-direction amplitude panning (MDAP) [ref.3]. A function implementing the variant vector-base intensity panning [ref.4] is also included. Recently, both VBAP and VBIP have been additionaly used for the design of robust ambisonic decoding matrices, see [ref.5&6].

The code is written by Archontis Politis, except the core vbap() function contributed by Ville Pulkki, with small modifications by Archontis Politis. The following code examples are meant to give a quick idea how to use the library for common operations in amplitude panning, such as triangulation of a 3D loudspeaker setup into loudspeaker triplets, spreading of a panned source, construction of panning gain tables, and panning a moving source in a real-time block processing context.

The library contains the following main functions:

findLsPairs:    find sorted loudspeaker pairs from loudspeaker
                directions (for 2D layouts)
findLSTriplets: find valid loudspeaker triangles from loudspeaker
                directions (for 3D layouts)
invertLsMtx:    precompute inversion of matrix of loudspeaker triplets
                or pairs, for use in VBAP
getSpreadSrcDirs:   get auxiliary source directions around panning
                    direction, for source spreading and MDAP
vbap:   Return VBAP panning gains for multiple panning directions, with
        spread control if needed

Additionaly:

plotTriangulation:  Plots the loudspeaker triangulated mesh
getGainTable:   Construct a look-up VBAP gain table of VBAP for a
                specified regular grid
vbip:   Similar to VBAP, but implementing its energy-based variant
        (see [ref.4])
getPValueResponse:  Returns VBAP frequency-dependent normalization
                    values, for approximate flat perceived response of
                    a panned source in dry playback environments
                    (see [ref.7])

For any questions, comments, corrections, or general feedback, please contact archontis.politis@aalto.fi

EXAMPLE 1: Triangulation

Triangulation of 3D setups is done using the convex hull of the loudspeaker points on the unit sphere (equivalent to Delaunay triangulation)

% FULL SPHERE EXAMPLE OF 29 SPEAKERS
ls_dirs_full = [-18 -54 -90 -126 -162 -198 -234 -270 -306 -342  0    -72  -144 -216 -288 -45  -135 -225 -315 0;
                 0   0   0   0    0    0    0    0    0    0   -10   -10  -10  -10  -10   45   45   45   45  90]';
% Delaunay triangulation
[~, ls_full] = findLsTriplets(ls_dirs_full);

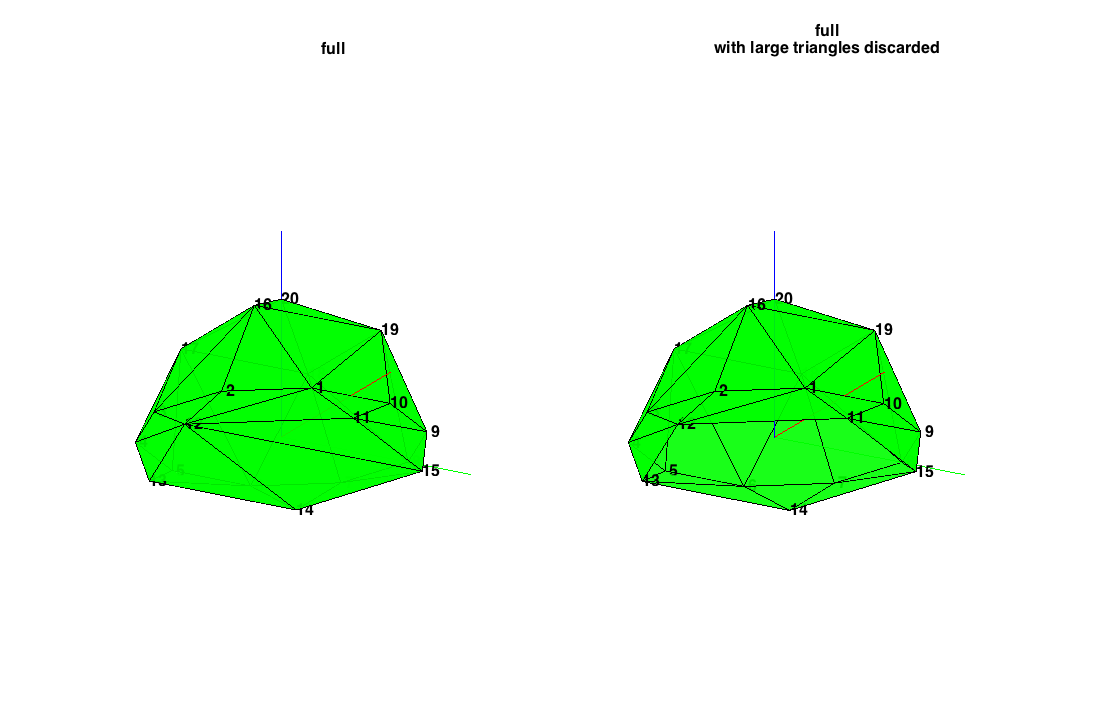
OMITTING LARGE TRIANGLES:

In many cases (like the setup above), it is advantageous to remove very large triangles (with aperture>~100deg) that are going to result in unstable localization, such as the ones below -10deg elevation in the example configuration above (see next plot). If you use this, always check visually the triangulation to be sure that you haven't omitted by mistake some triangle that you would like to keep. An alternative strategy is to introduce virtual loudspeakers that their channels are then either discarded or mixed with the actual ones.

% omit large triangles
OMIT_LARGE_TRI = 1;
large_tri_aperture = 100; % largest allowed triangle side in degrees
[~, ls_full_omit] = findLsTriplets(ls_dirs_full, OMIT_LARGE_TRI, large_tri_aperture);

% plot triangulations
figure
subplot(121)
plotTriangulation(ls_full)
title('full'), set(findall(gca, 'type', 'text'), 'visible', 'on', 'fontsize',16) % make title visible
view(60,-20), zoom(2)
subplot(122)
plotTriangulation(ls_full_omit)
title(['full' char(10) 'with large triangles discarded']), set(findall(gca, 'type', 'text'), 'visible', 'on', 'fontsize',16)
view(60,-20), zoom(2)
h = gcf; h.Position(3:4) = 2*h.Position(3:4);

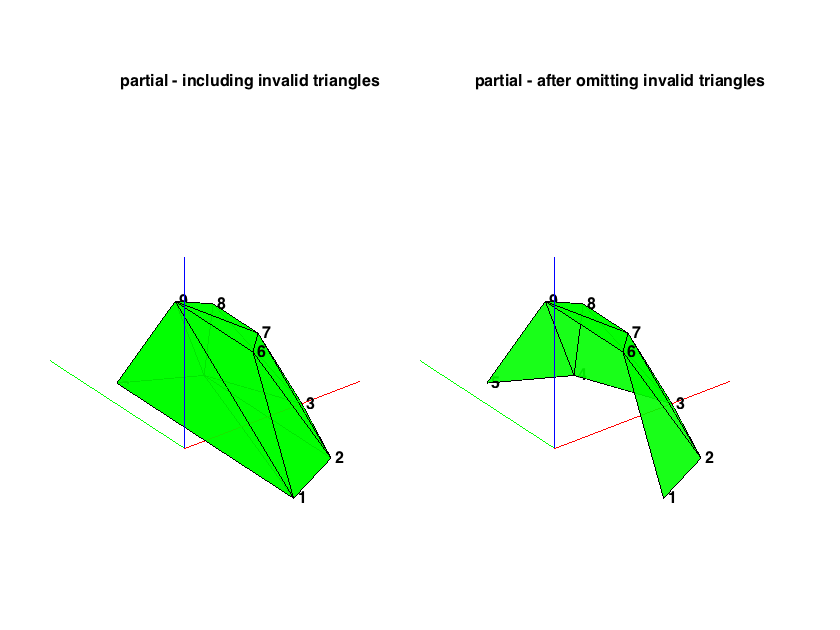
PARTIAL SETUP OF LOUDSPEAKERS

Partial setups can be domes, or setups around a screen, etc. In this case loudspeaker triplets should be discarded when their normals do not point outwards. This is handled automatically by the findLsTriplets() function.

% define a partial frontal setup
ls_dirs_partial = [-80 -45 0 45 80 -60 -30 30 60;
                    0   0  0 0  0   60  60 60 60]';
% triangulate directly, without considering invalid triangles
ls_dirs_rad = ls_dirs_partial*pi/180;
[tempx, tempy, tempz] = sph2cart(ls_dirs_rad(:,1), ls_dirs_rad(:,2), 1);
ls_part_invalid.vert = [tempx, tempy, tempz];
ls_part_invalid.faces = convhulln(ls_part_invalid.vert);
% trinagulate and discard invalid faces
[~, ls_part_valid] = findLsTriplets(ls_dirs_partial);

% plot triangulation
figure
subplot(121)
plotTriangulation(ls_part_invalid)
title('partial - including invalid triangles'), set(findall(gca, 'type', 'text'), 'visible', 'on', 'fontsize',16)
view(3), zoom(1.5)
subplot(122)
plotTriangulation(ls_part_valid)
title('partial - after omitting invalid triangles'), set(findall(gca, 'type', 'text'), 'visible', 'on', 'fontsize',16)
view(3), zoom(1.5)
h = gcf; h.Position(3:4) = 1.5*h.Position(3:4);

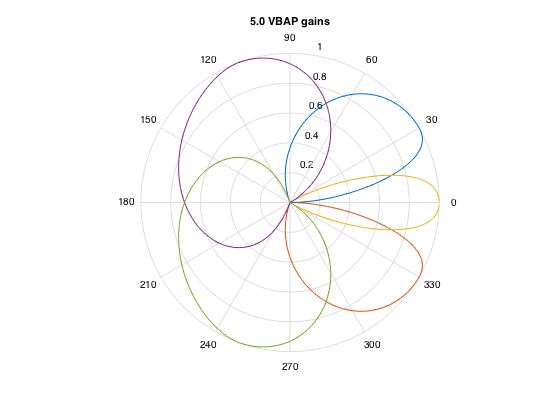
EXAMPLE 2: VBAP Gains

The steps to obtaining the VBAP gains for a set of directions are:

% a) define loudspeaker setup ls_dirs = [azi1 azi2 ... aziK] for 2D
%    or  ls_dirs = [azi1 elev1; azi2 elev2; ...; aziK elevK] for 3D
ls_dirs = [30 -30 0 110 -110]; % define a 2D 5.0 setup in degrees
%
% b) find valid loudspeaker pairs or triplets:
%    findLsPairs(ls_dirs) for 2D, or
%    findLsTriplets(ls_dirs) for 3D
ls_groups = findLsPairs(ls_dirs);
%
% c) compute inverse matrices for loudspeaker pairs or triplets, needs to
%    be done once for any panning direction
layoutInvMtx = invertLsMtx(ls_dirs, ls_groups);
%
% d) compute vbap gains for the required source directions, in degrees
src_dirs2D = (0:359)'; % 2D panning directions at every 1deg
gains2D = vbap(src_dirs2D, ls_groups, layoutInvMtx); % compute vbap gains

% Plot panning gains
figure
polar(src_dirs2D*ones(1,5)*pi/180, gains2D)
title('5.0 VBAP gains')

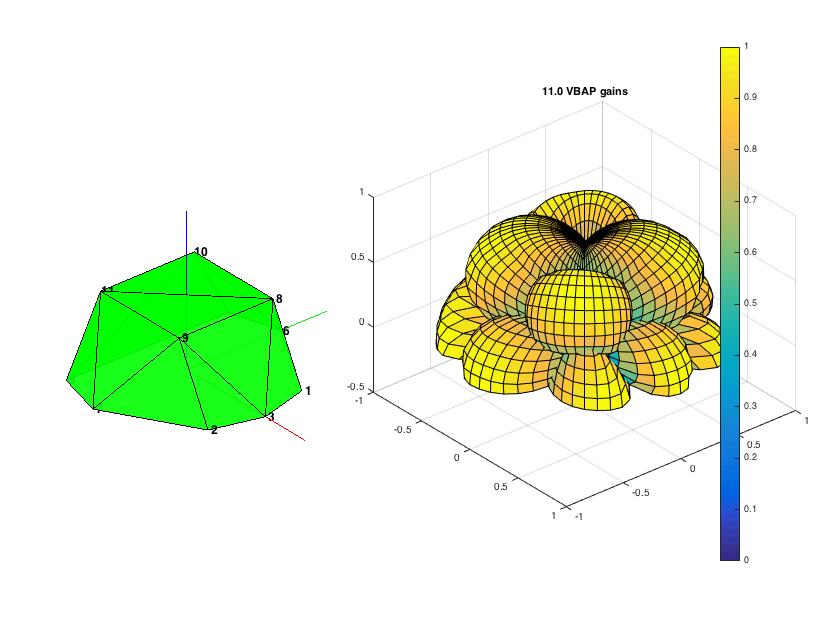
% Repeat process for an 11.0 3D setup
ls_dirs = [30 -30 0 120 -120 90 -90 45 -45 135 -135; 0 0 0 0 0 0 0 45 45 45 45]';
[ls_groups, layout] = findLsTriplets(ls_dirs); % return also triangulation mesh for plotting
figure, subplot(121), plotTriangulation(layout); view(50,30), zoom(2) % plot triangulation
layoutInvMtx = invertLsMtx(ls_dirs, ls_groups);
% Generate a regular 2D grid of panning directions covering the sphere
aziRes = 5;
elevRes = 5;
[Elev, Azi] = meshgrid(-90:elevRes:90, 0:aziRes:360);
src_dirs3D = [Azi(:) Elev(:)];
% Get VBAP gains
gains3D = vbap(src_dirs3D, ls_groups, layoutInvMtx);

% Plot panning gains
ls_num = size(ls_dirs,1);
[nAzi, nElev] = size(Azi);
[X,Y,Z] = sph2cart(Azi*pi/180,Elev*pi/180,1);
subplot(122)
hold on
for nl = 1:ls_num
    gains_grid_nl = reshape(gains3D(:,nl), nAzi, nElev);
    surf(gains_grid_nl.*X,gains_grid_nl.*Y,gains_grid_nl.*Z,gains_grid_nl);
end
axis([-1 1 -1 1 -0.5 1]), axis equal
colorbar, view(50,30), zoom(2), grid
title('11.0 VBAP gains')
h = gcf; h.Position(3:4) = 1.5*h.Position(3:4);

EXAMPLE 3: Spreading by amplitude panning

Spreading of sources by means of amplitude panning has two useful applications: a)creating synthetic sounds at arbitrary directions that have perceptually some spatial extent (see [ref.2&3]), and b)creating panning gains for multichannel systems that avoid the "loudspeaker detent" effect of sources collapsing to the loudspeakers or appearing spread at certain directions and very point-like at others (see [ref.3]). This second application is useful also on the design of stable hybrid ambisonic decoders (see [ref.6]).

Spread can be controlled if an extra spread parameter is added to the vbap() function. This parameter determines the extent of the source in degrees. The spread effect is created by using auxiliary spread sources around the main panning direction. If no additional arguments are passed along the desired spread, a default of 8 auxiliary sources are used. Otherwise, an arbitrary number of auxiliary sources can be generated by an additional argument num_spread_src. For 3D cases, the spread sources are arranged on a ring around the panning direction. By default, a single ring is used. More rings can be generated by an extra argument num_spread_rings.

% plot spread source directions for a 2D setup
spread = 60;
U_spread1 = getSpreadSrcDirs(-90, spread);
spread = 100;
num_spread_src = 32;
U_spread2 = getSpreadSrcDirs(45, spread, num_spread_src);
U_circle = [cos(0:pi/100:2*pi)' sin(0:pi/100:2*pi)'];
figure
plot(U_circle(:,1), U_circle(:,2), 'k')
hold on
plot(U_spread1(:,1), U_spread1(:,2), 'ro') % spread source 1
plot(U_spread2(:,1), U_spread2(:,2), 'bo') % spread source 2
axis equal, title('2D spread sources')

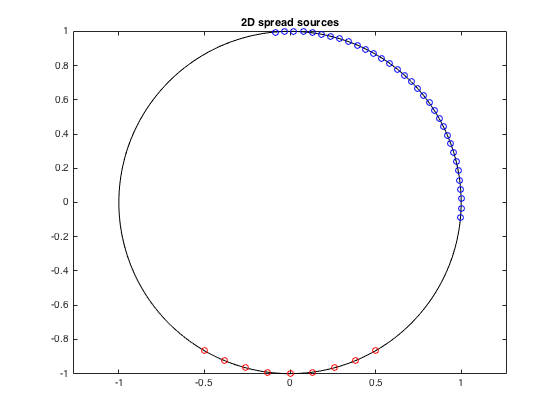
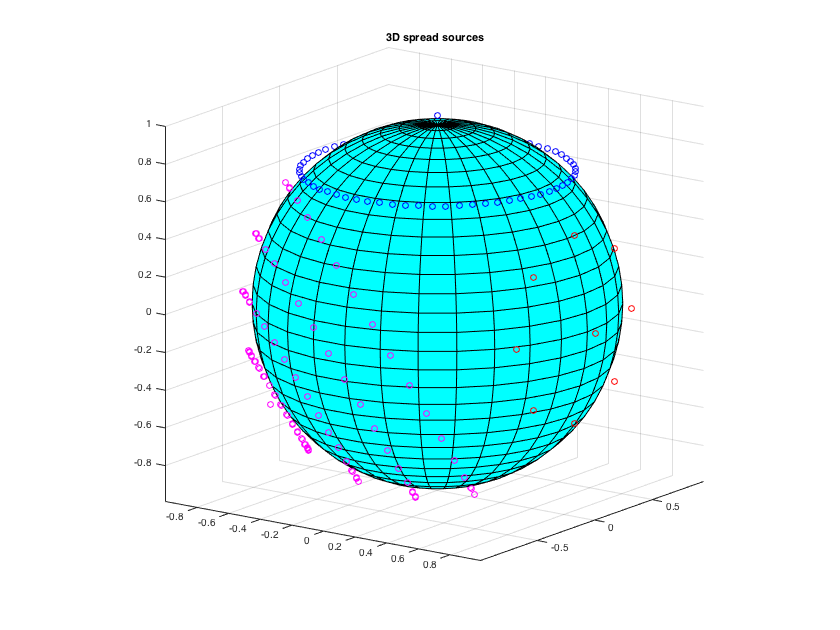
% plot spread source directions for a 3D setup
spread = 60;
U_spread1 = getSpreadSrcDirs([0 0], spread);
spread = 90;
num_spread_src = 64;
U_spread2 = getSpreadSrcDirs([0 90], spread, num_spread_src);
spread = 140;
num_spread_src = 32;
num_spread_rings = 4;
U_spread3 = getSpreadSrcDirs([-135 -30], spread, num_spread_src, num_spread_rings);

[Xs, Ys, Zs] = sphere(30);
figure
surf(0.95*Xs, 0.95*Ys, 0.95*Zs, 1, 'facecolor','c')
hold on
plot3(U_spread1(:,1), U_spread1(:,2), U_spread1(:,3), 'ro') % spread source 1
plot3(U_spread2(:,1), U_spread2(:,2), U_spread2(:,3), 'bo') % spread source 2
plot3(U_spread3(:,1), U_spread3(:,2), U_spread3(:,3), 'mo') % spread source 3
view(36,15), axis equal, title('3D spread sources')
h = gcf; h.Position(3:4) = 1.5*h.Position(3:4);

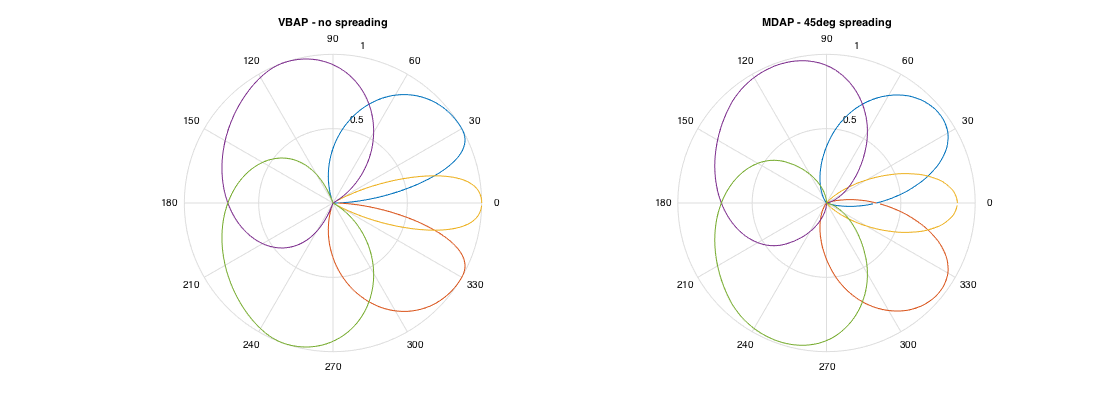
% compute 2D vbap gains for a 5.0 layout, with and without spreading
ls_dirs = [30 -30 0 110 -110]; % define a 2D 5.0 setup in degrees
ls_groups = findLsPairs(ls_dirs);
layoutInvMtx = invertLsMtx(ls_dirs, ls_groups);
src_dirs2D = (0:359)';
gains_nospread = vbap(src_dirs2D, ls_groups, layoutInvMtx);
spread = 45;
gains_spread = vbap(src_dirs2D, ls_groups, layoutInvMtx, spread);

% Plot panning gains
figure
subplot(121)
polar(src_dirs2D*ones(1,5)*pi/180, gains_nospread)
title('VBAP - no spreading')
subplot(122)
polar(src_dirs2D*ones(1,5)*pi/180, gains_spread)
title('MDAP - 45deg spreading')
h = gcf; h.Position(3) = 2*h.Position(3);

EXAMPLE 4: Gain Tables

For some applications it may be advantageous to precalculate a gain table of panning gains with some required spatial resolution, and then just look-up the gains for the panning direction. This is faster than computing the gains online but it requires more memory. Gain tables can be computed with the getGainTable() function.

% 2D gain table example and look-up
azi_res = 3; % compute gains at every 3 degrees (default 1deg if not defined)
ls_dirs = [30 -30 0 110 -110];
gtable2D = getGainTable(ls_dirs, azi_res);
% look-up gains for a certain direction
azi = 97.65;
idx2D = round(mod(azi+180,360)/azi_res)+1;
gains2D = gtable2D(idx2D,:);

% 3D gain table example and look-up
azi_res = 5;
elev_res = 5; % compute gains at every 5deg azimuth and elevation (default 2deg and 5deg respectively)
N_azi = round(360/azi_res) + 1;
ls_dirs = [30 -30 0 120 -120 90 -90 45 -45 135 -135; 0 0 0 0 0 0 0 45 45 45 45]';
gtable3D = getGainTable(ls_dirs, [azi_res elev_res]);
% look-up gains for a certain direction
azi = -123.6;
elev = 37.65;
aziIndex = round(mod(azi+180,360)/azi_res);
elevIndex = round((elev+90)/elev_res);
idx3D = elevIndex*N_azi+aziIndex+1;
gains3D = gtable3D(idx3D,:);

EXAMPLE 5: Moving source

A simple example of panning a moving source with block processing (one-and-a-half horizontal rotation of a 500Hz sinusoid, at 3 seconds).

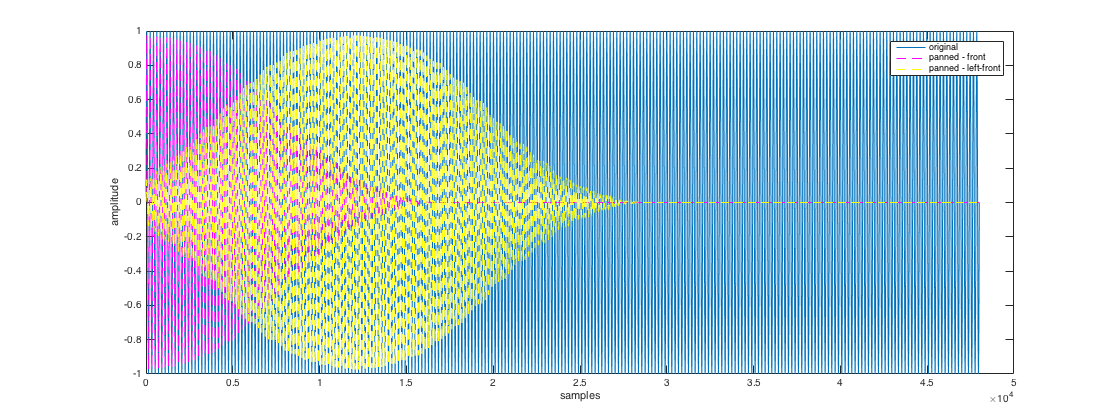
% initial parameters
fs = 48000; % samplerate
blocksize = fs/20; % (~50msec)
hopsize = blocksize/2; % panning hopsize (update the panning values twice per bocksize)
ls_dirs = [0  45 90  135 180 -135 -90 -45 0;    % define an octagon with a top
           0  0  0   0   0    0    0   0  90]'; % loudspeaker
ls_num = size(ls_dirs,1);

% define signal
sig = sin(2*pi*250*(1:3*fs)/fs)'; % 3sec of 250Hz sinewave as example
Lsig = length(sig);
Nhop = ceil(Lsig/hopsize) + 2;
padsig = [zeros(hopsize,1); sig; zeros(Nhop*hopsize - Lsig - hopsize,1)]; % zero padding
pansig = zeros(size(padsig,1), ls_num);

% define the trajectory for panning, one and a half horizontal rotation
azis = (0:(Nhop-1)-1)'*(1.5*360)/(Nhop-1);
eles = 0*azis;

% precompute VBAP triplet inversion
ls_groups = findLsTriplets(ls_dirs); % return also triangulation mesh for plotting
layoutInvMtx = invertLsMtx(ls_dirs, ls_groups);

% do panning of signal to defined trajectory with overlap-add method
counter = 1;
window = hanning(blocksize);
spread = 30;
for idx = 0:hopsize:(Nhop-2)*hopsize
    winsig = padsig(idx+(1:blocksize),1) .* window;
    azi = azis(counter);
    ele = eles(counter);
    gains = vbap([azi ele], ls_groups, layoutInvMtx, spread);
    panwinsig = winsig*gains;
    pansig(idx+(1:blocksize),:) = pansig(idx+(1:blocksize),:) + panwinsig;
    counter = counter+1;
end
% truncate loudspeaker signals to original length (omit zeropadding)
pansig = pansig(hopsize+(1:Lsig),:);

% plot original signal and panned front and front-left channel, half rotation only
figure, plot(1:Lsig/3, sig(1:Lsig/3), 1:Lsig/3, pansig(1:Lsig/3,1), '--m', 1:Lsig/3, pansig(1:Lsig/3,2), '--y');
legend('original','panned - front', 'panned - left-front'), xlabel('samples'), ylabel('amplitude')
h = gcf; h.Position(3) = 2*h.Position(3);

% write audio output to file
audiowrite('panning_example.wav', pansig, fs)

EXAMPLE 6: VBAP filters with frequency-dependent P-value

Commonly VBAP is used with a frequency-independent power normalization of the amplitude panning gains, assuming incoherent summation of the speaker channels at the listener's ears, in order to result in a constant perceived loudness with panning direction. This assumption is on average valid for most domestic listening environments and for mid-to high frequencies.

More generally, the gain normalization factor for L loudspeakers can be defined as

$N = \sum_{l=1}^{L} \sqrt[p]{ g_l^p}, \quad p\in[0,1]$

where p=1 corresponds to amplitude normalization and p=2 to standard power normalization. Amplitude normalization is more appropriate at low frequencies and in dry playback environments due to coherent summation of the loudspeaker channels. Power normalization can cause a clearly perceived bass-boosting effect in these cases.

A solution is proposed in [ref.7], where the p-value becomes frequency-dependent, with respect to a room-related parameter corresponding roughly to the direct-to-total energy ratio. The function getPValueResponse() returns these normalization values at specified frequencies, and the code below demonstrates how it can be used to construct VBAP gain filters.

fs = 40000; % sample rate
Lfilt = 512; % filter length (unnecessary long - used for smooth plots below)

f = (0:Lfilt/2)*fs/Lfilt; % frequency vector
DTT = 1; % 1 for anechoic conditions, ~0.5 for listening rooms, 0 for standard power normalization
pValue = getPValueResponse(f, DTT);
ls_dirs5 = [30 -30 0 110 -110];
gains = vbap(15, findLsPairs(ls_dirs5),invertLsMtx(ls_dirs5, findLsPairs(ls_dirs5))); % VBAP gains for source at 15deg
ls_num = length(ls_dirs5);
for nf=1:Lfilt/2+1
    pv_f = pValue(nf); % p-value for this frequency
    H_filt(nf,:) = gains./((sum(gains.^pv_f)).^(1/pv_f) * ones(1,ls_num));
end
% get impulse response
h_filt = fftshift(ifft([H_filt; H_filt(end-1:-1:2,:)]),1);

% plot the p-value curve and the magnitude response of the filter for the
% left speaker
figure
subplot(121), semilogx(f, pValue), grid, axis([100 2e4 1 2]), title(['p-value for DTT=' num2str(DTT)])
subplot(122), semilogx(f, H_filt(:,1)), grid, axis([100 2e4 0 1]), title('|H_{vbap}| for left speaker')
h = gcf; h.Position(3) = 2*h.Position(3);

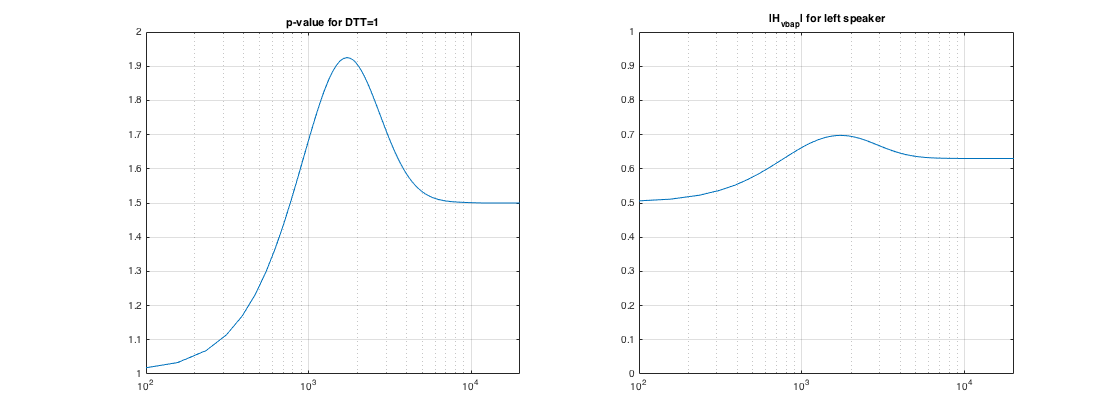
Note that the experimental curves of [ref.7] are derived for listening with pairs of loudspeakers, however the authors have used them with success also in 3D loudspeaker setups.

REFERENCES

[1] Pulkki, V. (1997). Virtual Sound Source Positioning Using Vector Base Amplitude Panning. Journal of the Audio Engineering Society, 45(6), 456-466.

[2] Pulkki, V. (2000). Generic panning tools for MAX/MSP. International Computer Music Conference (ICMC), Berlin, Germany

[3] Pulkki, V. (1999). Uniform Spreading of Amplitude Panned Sources. IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (WASPAA), New Paltz, NY, USA

[4] Jot, J.-M., Larcher V., Pernaux, J.-M. (1999). A comparative study of 3-D audio encoding and rendering techniques. 16th International Conference of the AES, Rovaniemi, Finland

[5] Zotter, F., Frank, M. (2012). All-Round Ambisonic Panning and Decoding. Journal of the Audio Engineering Society, 60(10), 807-820.

[6] Epain, N., Jin, C.T., Zotter, F. (2014). Ambisonic Decoding With Constant Angular Spread. Acta Acustica united with Acustica, 100(May), 928-936.

[7] Laitinen, M., Vilkamo, J., Jussila, K., Politis, A., Pulkki, V. (2014). Gain normalization in amplitude panning as a function of frequency and room reverberance. 55th International Conference of the AES. Helsinki, Finland.