On Minimizing the Look-Up Table Size in Quasibandlimited Classical Waveform Oscillators

Abstract

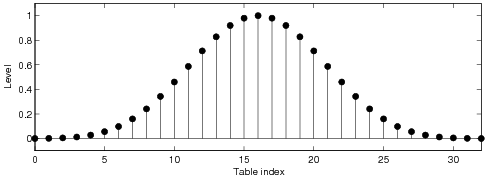
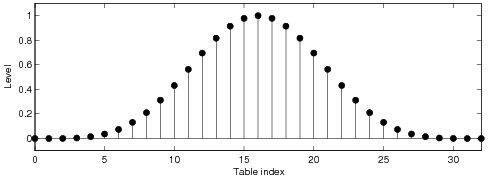
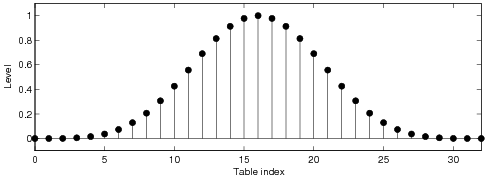
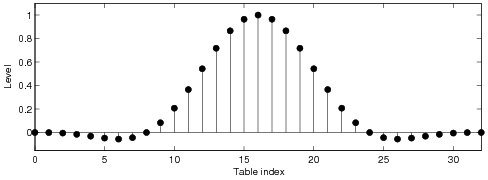
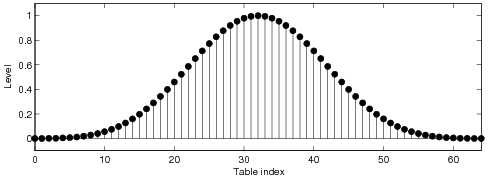
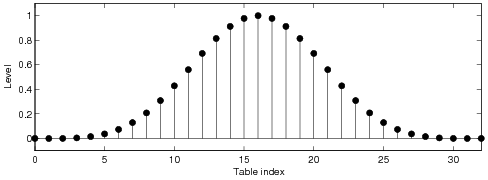
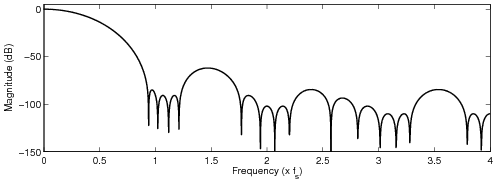
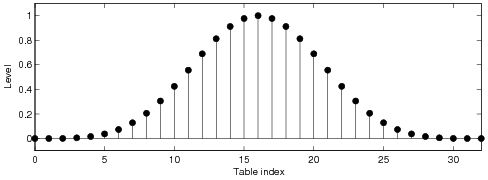
In quasi bandlimited classical waveform oscillators, the aliasing distortion present in a trivially sampled waveform can be reduced in the digital domain by applying a tabulated correction function. This paper concerns an approach that applies the correction function in differentiated domain by synthesizing a bandlimited impulse train (BLIT) that is integrated to obtain the desired bandlimited waveform. 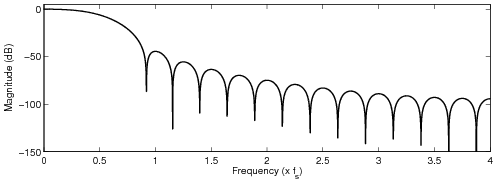The ideal correction function of the BLIT method is infinitely long and in practice it needs to be truncated and windowed. 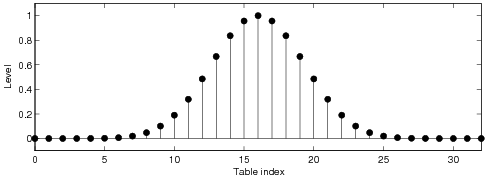In order to obtain a good alias reduction performance, long tables are typically required. It is shown that when a short look-up table is used, a windowed ideal correction function does not provide the best alias reduction performance. 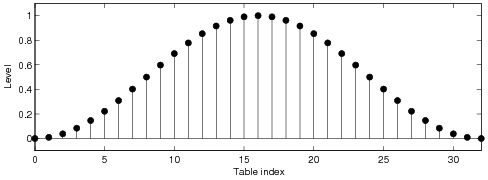Instead, a better alias reduction performance can be obtained with a look-up table that has a parametric control over the low-order generations of aliasing. Some practical parametric look-up table designs are discussed in this paper, and their use and alias reduction performance are exemplified. The look-up table designs discussed in this paper that provide the best alias reduction performance are parametric window functions and the least-squares optimized multi-band FIR filter designs. The presented look-up tables and sound examples on their alias reduction performance can be found from http://www.acoustics.hut.fi/go/dafx10-optosctables/.

Keywords

Subtractive sound synthesis, oscillator algorithms, bandlimited impulse synthesis, look-up table design

Files

• Conference paper (PDF, 540 KiB)
• Presentation slides (PDF, 585 KiB)

Demos

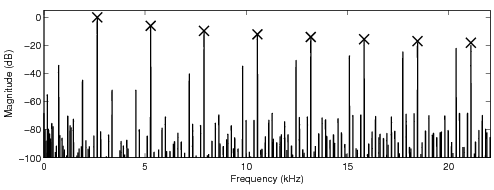
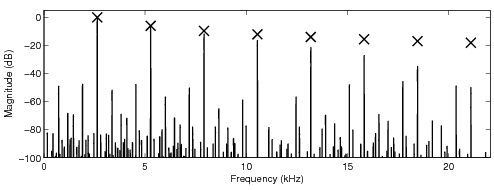
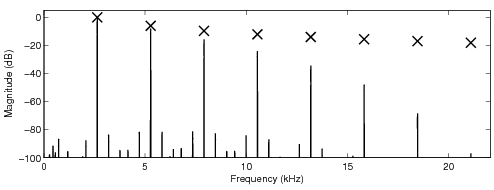
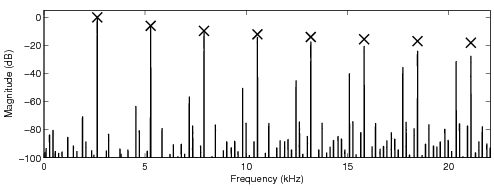
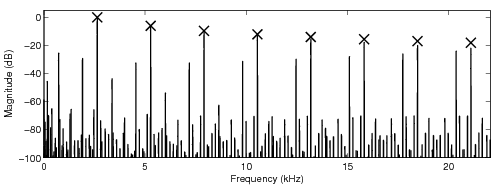
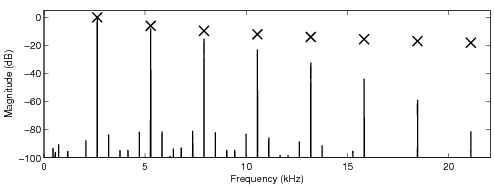
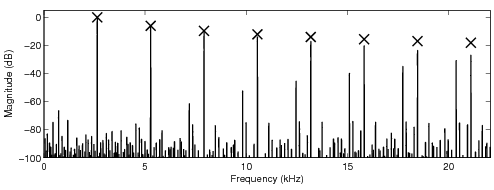
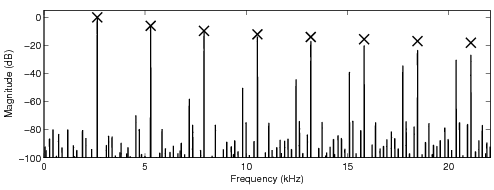
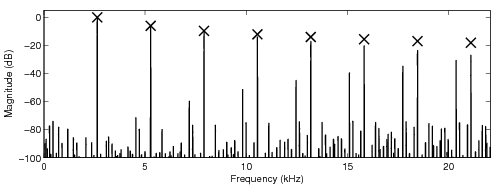
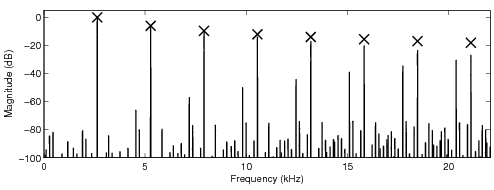
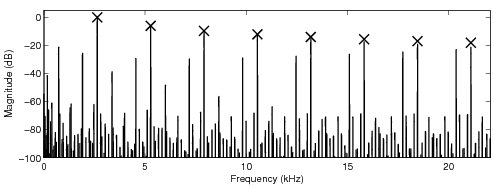
In the following sound examples, the fundamental frequency of the sawtooth waveform is 2.673 kHz. A sampling frequency 44.1 kHz was used. The number of samples the look-up tables modify is four (4) if not stated otherwise, and an oversampling factor eight (8) is used in all tables. The other parameters for the look-up table are given before the sound examples. The crosses in the sawtooth spectra indicate the desired levels of the harmonics of the ideal bandlimited sawtooth waveform.

References

• Trivially sampled sawtooth
• Ideally bandlimited sawtooth (Additive synthesis approach, requires 8 sinusoidal oscillators, computationally inefficient)

Hann-windowed sinc function

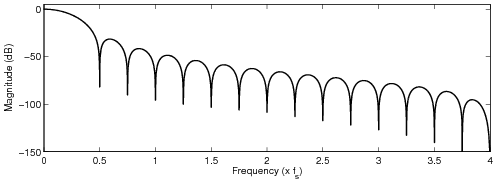
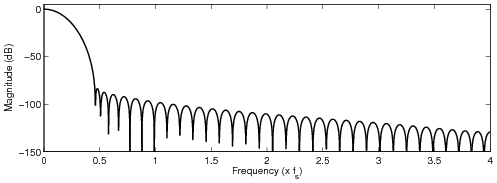
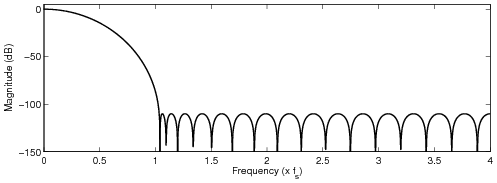
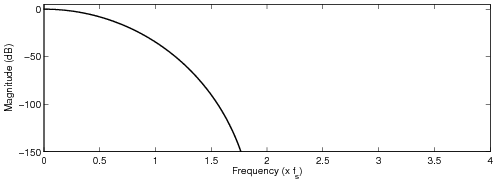
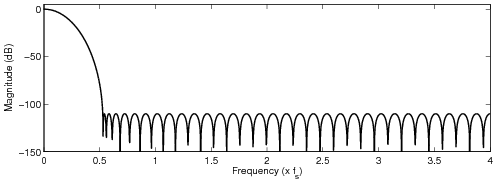
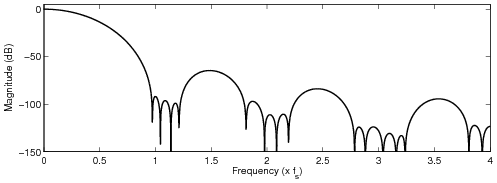
The cutoff frequency was set to the Nyquist frequency.

Look-up table (as plain text)	Frequency response of the look-up table
BLIT sawtooth spectrum (waveform as a wav file)

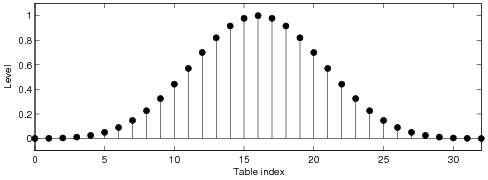
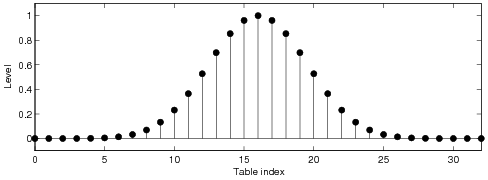
Plain Hann window

Look-up table (as plain text)	Frequency response of the look-up table
BLIT sawtooth spectrum (waveform as a wav file)

Kaiser windows

Modifies four (4) samples, minimum stopband attenuation 110 dB

Look-up table (as plain text)	Frequency response of the look-up table
BLIT sawtooth spectrum (waveform as a wav file)

Modifies four (4) samples, minimum stopband attenuation 220 dB

Look-up table (as plain text)	Frequency response of the look-up table
BLIT sawtooth spectrum (waveform as a wav file)

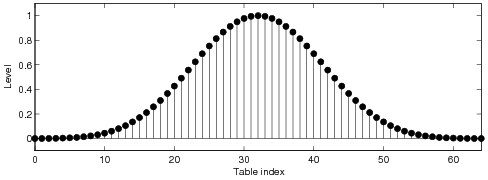
Modifies eight (8) samples, minimum stopband attenuation 110 dB

Look-up table (as plain text)	Frequency response of the look-up table
BLIT sawtooth spectrum (waveform as a wav file)

Chebyshev windows

Modifies four (4) samples, minimum stopband attenuation 110 dB

Look-up table (as plain text)	Frequency response of the look-up table
BLIT sawtooth spectrum (waveform as a wav file)

Modifies four (4) samples, minimum stopband attenuation 220 dB

Look-up table (as plain text)	Frequency response of the look-up table
BLIT sawtooth spectrum (waveform as a wav file)

Modifies eight (8) samples, minimum stopband attenuation 110 dB

Look-up table (as plain text)	Frequency response of the look-up table
BLIT sawtooth spectrum (waveform as a wav file)

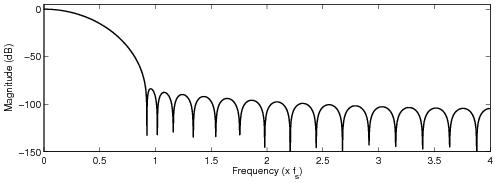
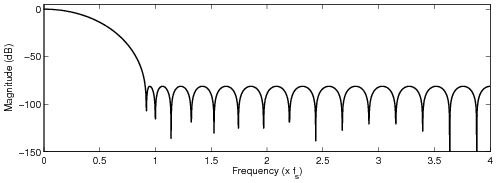
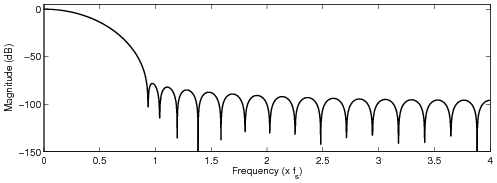
Optimized FIR filter designs

All the following examples modify four (4) samples. The maximum allowed passband attenuation was set to 6 dB at 15 kHz, and the stopband was set from 5 kHz below the sampling frequency to the upsampled Nyquist frequency. In the frequency-weighted designs, more weight was given for the stopband frequencies that fold back between DC and 10 kHz. Moreover, a spectral tilt was included in the frequency-dependent weight, see the paper for detailed discussion.

Minimax optimization, no frequency weighting

Look-up table (as plain text)	Frequency response of the look-up table
BLIT sawtooth spectrum (waveform as a wav file)

Least-squares optimization, no frequency weighting

Look-up table (as plain text)	Frequency response of the look-up table
BLIT sawtooth spectrum (waveform as a wav file)

Minimax optimization, with frequency weighting

Look-up table (as plain text)	Frequency response of the look-up table
BLIT sawtooth spectrum (waveform as a wav file)

Least-squares optimization, with frequency weighting

Look-up table (as plain text)	Frequency response of the look-up table
BLIT sawtooth spectrum (waveform as a wav file)