Benoit Alary, Archontis Politis, and Vesa Välimäki
Velvet Noise Decorrelator
Companion page for a paper in the 20th International Conference on Digital Audio Effects, at the University of Edinburgh on 5th - 9th September 2017
Abstract
The decorrelation of sound signals is an important process in the spatial reproduction of sounds. For instance, when a mono signal is spread on multiple loudspeakers, it should be decorrelated for each channel to avoid undesirable comb filtering artifacts. The process of decorrelating the signal itself is a compromise aiming to reduce the correlation as much as possible while minimizing both the sound coloration and the computing cost. A popular decorrelation method is convolving a sound signal with a short sequence of exponentially decaying white noise, but it requires the use of the FFT for fast convolution, which causes some latency. Here we propose a decorrelator based on a sparse random sequence called velvet noise, which achieves comparable results without latency and at a smaller computing cost. A segmented temporal decay envelope can also be implemented for further optimizations. Using the proposed method, we found that a decorrelation filter, of similar perceptual attributes to white noise, could be implemented using 83% less operations. Informal listening tests suggest that the resulting decorrelation filter performs comparably to an equivalent white noise filter.
Paper
The paper will be made available soon.Examples
The samples on this webpage have been generated using a MatLab implementation of the proposed algorithm.
The exponential decay examples are convolved with the following velvet sequence. The impulses are linearly distributed but the attenuation is decaying exponentially. 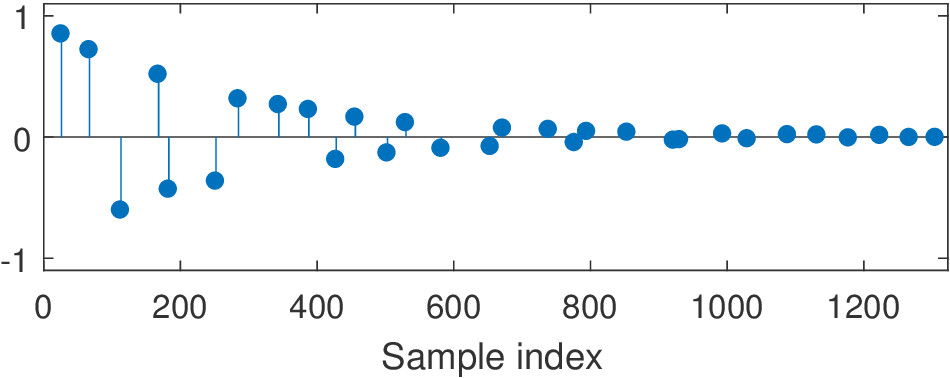
The logarithmic distribution examples are convolved with the following velvet sequence. The amplitude decay uses the segmented decay. 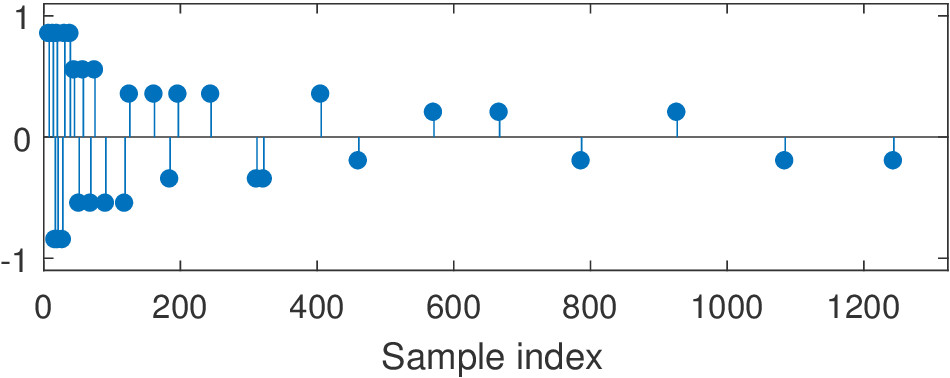
The segmented decay examples are convolved with the following velvet sequence. Four segments are used. 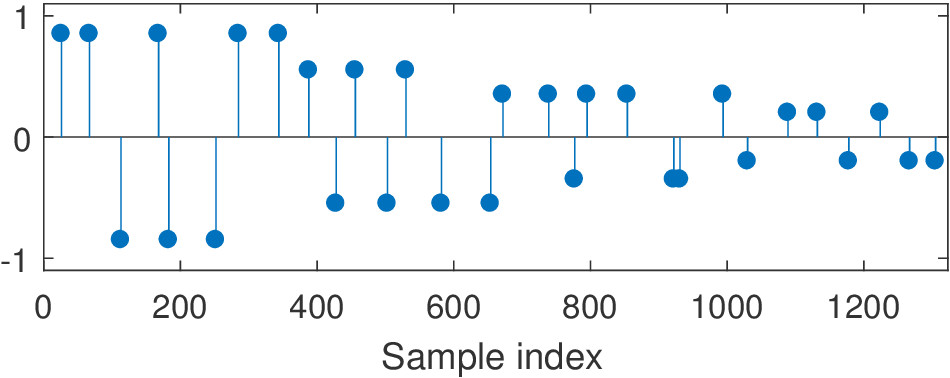
| Guitar | Song | Castanets | |
|---|---|---|---|
Original |
|||
White noise |
|||
Exponential decay |
|||
Logarithmic distribution |
|||
Segmented decay |
|
http://research.spa.aalto.fi/publications/papers/dafx17-vnd/ Updated on June 21, 2017 This page uses HTML5, CSS, and JavaScript |