Polynomial Transition Regions (PTR)
“Reducing Aliasing from Synthetic Audio Signals using Polynomial Transition Regions,”
to appear in IEEE Signal Processing Letters.
Source Code
- Python source for the algorithms, figures and sound examples from the paper (includes additional examples discussed below).
- Benchmark code as Pure Data (Pd) externals
Audio Examples
The audio examples are 16-bit signed PCM wavs, sampling rate is 44.1 kHz.
| Sound | Description | Parameters | Size (MB) |
|---|---|---|---|
| Square wave | trivial (3s) - pause (1s) - PTR W = 3 (3s) | f0 = 2490 Hz, r = 3.5 | 0.6 |
| Pulse Width Modulation | trivial (4s) - pause (1s) - PTR W = 3 (4s) | f0 = 698 Hz, Triangular LFO = 0.25 Hz | 0.78 |
| XOR synthesis | trivial (3s) - pause (1s) - PTR W = 3 (3s) | f0 = 500 Hz, see below for other parameters | 0.6 |
| Transients | Fig.3: DPW N = 3 (6s) - pause (1s) - PTR W = 2 (6s) | f0 = 500 Hz to 750 Hz, ramp-like fm = 10 Hz | 1.09 |
| Hardsync | Fig.4: trivial (3s) - pause (1s) - PTR W = 3 (3s) | fmaster = 1660 Hz, r = 1.5 | 0.6 |
| Hardsync sweep | Fig.4: trivial (3s) - pause (1s) - PTR W = 3 (3s) | fmaster = 1000 Hz → 1500 Hz, r = 3.5 | 0.6 |
DPW Correction Polynomials
DPW correction polynomials (Eq.7) as function of distance from the discontinuity D(n) = ϕ(n)P0 = ϕ(n)/T0.
| W | Span | Correction polynomial cW(D) |
| 1 | 0 T0 | 2D + 2 |
| 2 | 0 T0 | D2 4D + 4 |
| 2 | T0 2T0 | D2 + 2 |
| 3 | 0 T0 | D3/3 + 2 |
| 3 | T0 2T0 | 2D3/3 3D2 + 3D + 1 |
| 3 | 2T0 3T0 | D3/3 + 3D2 9D + 9 |
Further Application Examples
Pulse Waveform
The figure below shows that the aliasing contained in the trivial square wave (a), f0 = 2490 Hz, fs = 44100 Hz is suppressed substantially when using PTR of (b) W = 1, (c) W = 2, and (d) W = 3. The transition polynomials can be derived from Table 1 in the paper, and they are available in the Python source code release. Sound examples of the pulse waveform depicted below and of a pulse-width modulated timbre are available in the Audio Examples section above.

XOR Synthesis
XOR synthesis [1] applies bitwise exclusive-or operation between two audio signals. It is an efficient and versatile method, which unfortunately suffers from excessive aliasing. This has thus far reduced the usability of the method in musical audio contexts. PTR seems to mitigate the aliasing problems, opening the XOR method for further research efforts.
In the example below, bitwise XOR operation is applied between a bipolar sawtooth waveform (red, f0 = 500 Hz) and a square wave (green, f0 = 500 Hz), fs = 44100 Hz. The output waveform (thick black) onsists of two parts: a full-cycle ramp followed by its phase-shifted replica. As can be seen, although the output spectrum is contaminated with notorioius aliasing distortion, partials 2,6,10,14,... seems to be missing.
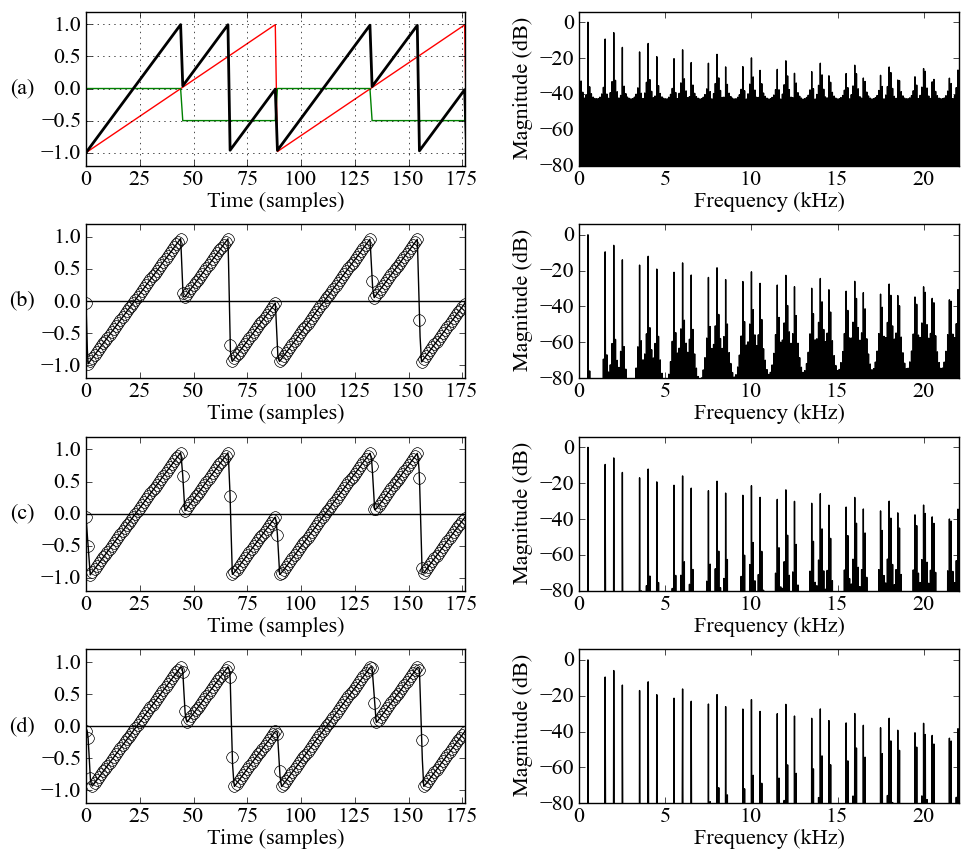
This is indeed the case, as shown in the PTR cleanups (b) W = 1, (c) W = 2, and (d) W = 3. The process was two-pass: the algorithm computes first the trivial aliasing contaminated input signal (a), and then applies the scaled and offset transition polynomials to the transition regions, leaving the other parts of the original signal intact (as given by Eq.(8)).
References
[1] Kleimola, J., "Audio Synthesis by Bitwise Logical Modulation", in Proc. of the 11th Int. Conf. on Digital Audio Effects (DAFx-08), pp.67-70, Espoo, Finland, September, 2008.
Contact
Please send your comments and remarks to the first author: firstname.lastname[-at-]aalto.fi
Page last modified Nov-09-2011.