Note that this is an old webpage, please CLICK HERE to be redirected to the new one.

Spatial Audio Real-time Applications (SPARTA)

About

SPARTA is a collection of flexible VST audio plug-ins for spatial audio production, reproduction and visualisation, developed primarily by members of the Acoustics Lab at Aalto University, Finland.

• Download links of current and past versions can be found here.

• The suite has been formally presented in this publication, with the source code made available here (GPLv3 license).

• The SPARTA installer also includes the COMPASS suite, the HO-DirAC suite, CroPaC Binaural Decoder, and the HO-SIRR room impulse response renderer. These plug-ins employ parametric processing and are signal-dependent, aiming to go beyond conventional linear Ambisonics by extracting meaningful parameters over time and subsequently employing them to map the input to the output in a more informed manner.

• For the curious researchers and/or spatial audio developers: note that the plugins included in the SPARTA installer are all built using the open-source Spatial_Audio_Framework (SAF).

List of plug-ins included in the SPARTA installer

The SPARTA suite:

• sparta_ambiBIN - A binaural ambisonic decoder (up to 7th order) with a built-in SOFA loader and head-tracking support via OSC messages. Includes: Least-Squares (LS), spatial re-sampling (SPR), time-alignment (TA), and magnitude least-squares (Mag-LS) decoding options.

• sparta_ambiDEC - A frequency-dependent loudspeaker ambisonic decoder (up to 7th order) with user specifiable loudspeaker directions (up to 64), which may be optionally imported via JSON configuration files. Includes: All-Round (AllRAD), Energy-Preserving (EPAD), Spatial (SAD), and Mode-Matching (MMD) ambisonic decoding options. The loudspeaker signals may also be binauralised for headphone playback.

• sparta_ambiDRC - A frequency-dependent dynamic range compressor for ambisonic signals (up to 7th order).

• sparta_ambiENC - An ambisonic encoder/panner (up to 7th order), with support for up to 64 input channels; the directions for which may also be imported via JSON configuration files.

• sparta_ambiRoomSim - A shoebox room simulator based on the image-source method, supporting multiple sources and ambisonic receivers..

• sparta_array2sh - A microphone array spatial encoder (up to 7th order), with presets for several commercially available A-format and higher-order microphone arrays. The plug-in can also present objective evaluation metrics for the currently selected configuration.

• sparta_beamformer - A spherical harmonic domain beamforming plug-in with multiple beamforming strategies (up to 64 output beams).

• sparta_binauraliser - A binaural panner (up to 64 input channels) with a built-in SOFA loader and head-tracking support via OSC messages.

• sparta_decorrelator - A simple multi-channel signal decorrelator (up to 64 input channels).

• sparta_dirass - A sound-field visualiser based on re-assigning the energy of beamformers. This re-assigment is based on DoA estimates extracted from "spatially-constrained" regions, which are centred around each beamformer look-direction.

• sparta_matrixconv - A basic matrix convolver with an optional partitioned convolution mode. The user need only specify the number of inputs and load the filters via a wav file.

• sparta_multiconv - A basic multi-channel convolver with an optional partitioned convolution mode. Unlike "MatrixConv", this plug-in does not perform any matrixing. Instead, each input channel is convolved with the respective filter; i.e. numInputs = numFilters = numOutputs.

• sparta_panner - A frequency-dependent 3-D panner using the VBAP method (up to 64 inputs and outputs).

• sparta_powermap - A sound-field visualisation plug-in based on ambisonic signals as input (up to 7th order), with PWD/MVDR/MUSIC/Min-Norm options.

• sparta_rotator - A flexible ambisonic rotator (up to 7th order) with head-tracking support via OSC messages.

• sparta_sldoa - A frequency-dependent sound-field visualiser (up to 7th order), based on depicting the direction-of-arrival (DoA) estimates derived from spatially localised active-intensity vectors. The low frequency estimates are shown with blue icons, mid-frequencies with green, and high-frequencies with red.

• sparta_spreader - An arbitrary array (e.g. HRIRs or microphone array IRs) panner with coherent and incoherent spreading options.

The COMPASS suite:

• compass_binaural - A binaural ambisonic decoder (up to 3rd order input) based on the parametric COMPASS model, with a built-in SOFA loader and head-tracking support via OSC messages.

• compass_binauralVR - Same as the compass_binaural plugin, but also supporting listener translation around the receiver position and support for multiple simultaneous listeners.

• compass_decoder - A parametrically enhanced loudspeaker ambisonic decoder (up to 3rd order input).

• compass_gravitator - A parametric sound-field focussing plug-in.

• compass_sidechain - A plug-in that manipulates the spatial properties of one Ambisonic recording based on the spatial analysis of a different recording.

• compass_spatedit - A flexible spatial editing plug-in.

• compass_tracker - A multiple target acoustic tracker which can optionally steer a beamformer towards each target.

• compass_upmixer - An Ambisonic upmixer (1-3rd order input, 2-7th order output).

The HO-DirAC suite (see license):

• hodirac_binaural - A binaural ambisonic decoder (up to 3rd order input) based on the parametric HO-DirAC model, with a built-in SOFA loader and head-tracking support via OSC messages.

• hodirac_decoder - A parametrically enhanced loudspeaker ambisonic decoder (up to 3rd order input).

• hodirac_upmixer - An Ambisonic upmixer (1-3rd order input, 2-7th order output).

Other:

• cropac_decoder - A binaural 1st order ambisonic decoder based on the parametric CroPaC model, with a built-in SOFA loader and head-tracking support via OSC messages.

• HOSIRR - An Ambisonic room impulse response (RIR) renderer for arbitrary loudspeaker setups, based on the Higher-order Spatial Impulse Response Rendering (HO-SIRR) algorithm; more information can be found here.

Detailed descriptions of the SPARTA Plug-ins

All plug-ins are tested using REAPER (64-bit), which is a very affordable and flexible DAW and is currently the only recommended host for these plug-ins; although, other hosts are also known to work. Currently, the plug-ins support sampling rates of 44.1 or 48kHz. All spherical harmonic-related plug-ins conform to the Ambisonic Channel Number (ACN) ordering convention and offer support for both orthonormalised (N3D) and semi-normalised (SN3D) normalisation schemes; note that the AmbiX format uses ACN/SN3D. The maximum transform order for these plug-ins is 7.

You may also hover your mourse cursor over any of the combo boxes/sliders/toggle buttons etc., in order to be presented with helpful tooltips regarding the purpose of the parameter.

Thanks to help from Daniel Rudrich, the relevant plug-ins now also support importing and exporting of loudspeaker, source, and sensors directions via .json configuration files; allowing for cross-compatibility between SPARTA and the IEM Ambisonics plug-in suite. More information regarding the structure of these files can be found here.

The default HRIR set is an 836-point simulation of a Kemar Dummy head, courtesy of Genelec AuralID.

SPARTA | AmbiBIN

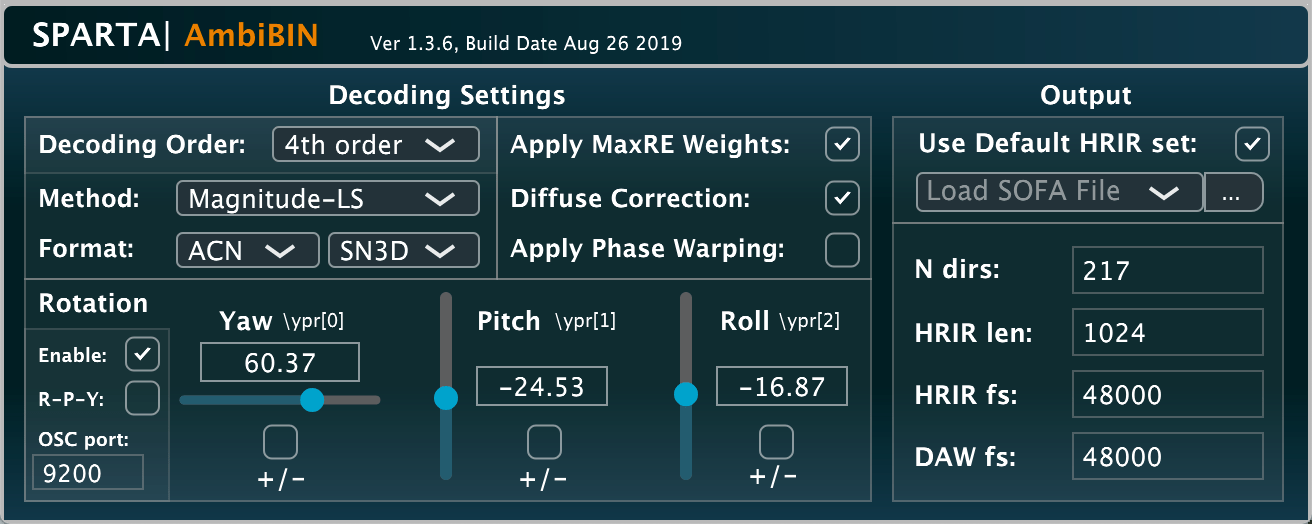
A binaural Ambisonic decoder for headphone playback of Ambisonic signals (aka spherical harmonic or B-format signals), with a built-in rotator and head-tracking support via OSC messages. The rotation angles are updated after the time-frequency transform, which allows for reduced latency compared to its loudspeaker counterpart 'AmbiDEC' when paired with 'Rotator'. The plug-in also allows the user to import their own HRIRs via the SOFA standard. The plug-in offers a variety of different decoding methods, including: Least-Squares (LS), Spatial re-sampling (SPR), Time-Alignment (TA) [11], and Magnitude Least-Squares (MagLS) [12]. It can also impose a diffuse-coherence contraint/correction on the current decoder, as described in [11].

This plug-in was developed by Leo McCormack, Archontis Politis, and Christoph Hold.

SPARTA | AmbiDEC

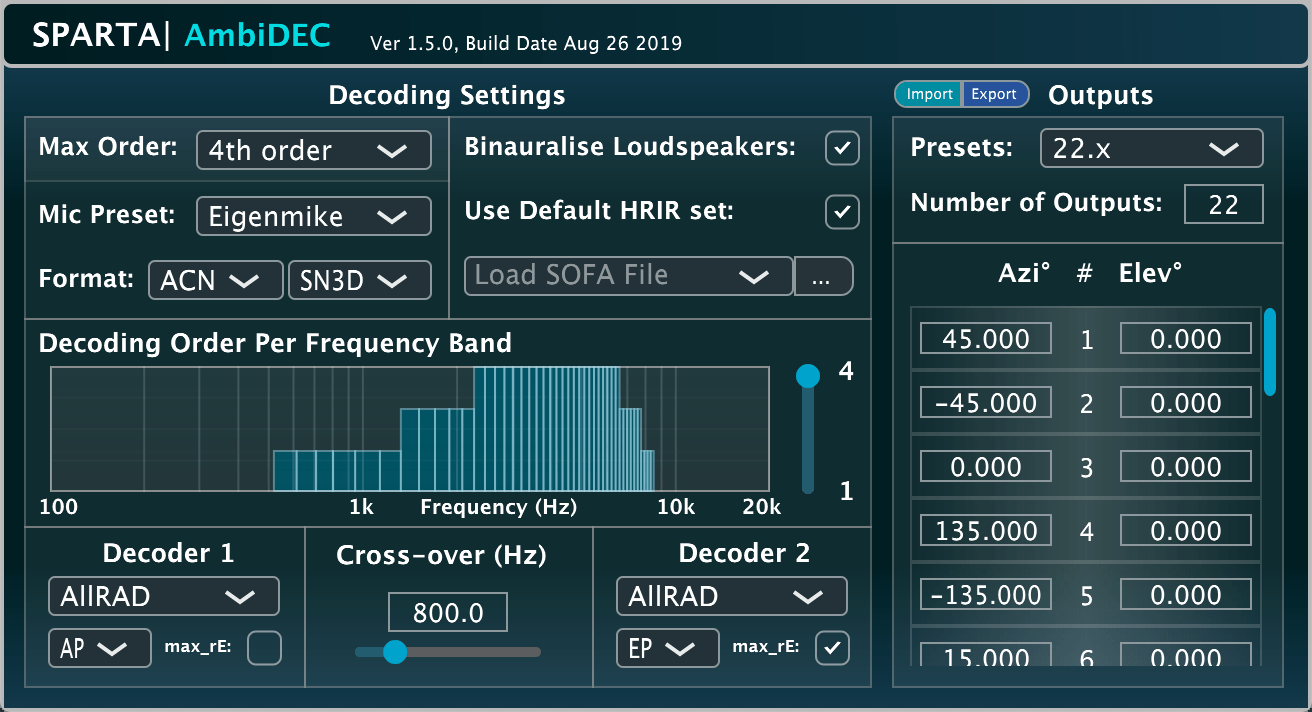
A frequency-dependent Ambisonic decoder for loudspeakers. The loudspeaker directions can be user-specified for up to 64 channels, or alternatively presets for popular 2D and 3D set-ups can be selected. For headphone reproduction, the loudspeaker audio is convolved with interpolated HRTFs for each loudspeaker direction (i.e. virtual loudspeaker decoding). The plug-in also permits importing custom HRIRs via the SOFA standard.

The plug-in employs a dual decoding approach, whereby different decoder settings may be selected for the low and high frequencies; the cross-over frequency may be dictated by the user. Several ambisonic decoders have been integrated, including more perceptually motivated methods such as the All-Round Ambisonic Decoder (AllRAD) [1] and Energy-Preserving Ambisonic Decoder (EPAD) [2]. The max-rE weighting [1] may also be enabled for either decoder. Furthermore, in the case of non-ideal Ambisonic signals as input (i.e. those derived from physical/simulated microphone arrays), the decoding order may be specified for the appropriate frequency ranges; energy-preserving (EP) or amplitude-preserving (AP) normalisation is then used to maintain consistent loudness between different decoding orders. However, this feature may also be used creatively. For example, one can reduce the decoding order only for a certain frequency-range, thereby making the reproduction more spatially spread at these specific frequencies (due to the inherently lower spatial resolution when using lower-order Ambisonic signals for decoding).

Note that when the loudspeakers are uniformly distributed (e.g. a t-design), all of the decoding approaches implemented in the plug-in are equivelent. This can be effectively demonstrated by selecting a T-design loudspeaker set-up (a nearly-uniform distribution of points on a sphere). The benefits of the Mode-Matching decoding (MMD), AllRAD and EPAD approaches can be observed for non-uniform arrangements (22.x for example).

This plug-in was developed by Leo McCormack and Archontis Politis.

SPARTA | AmbiDRC

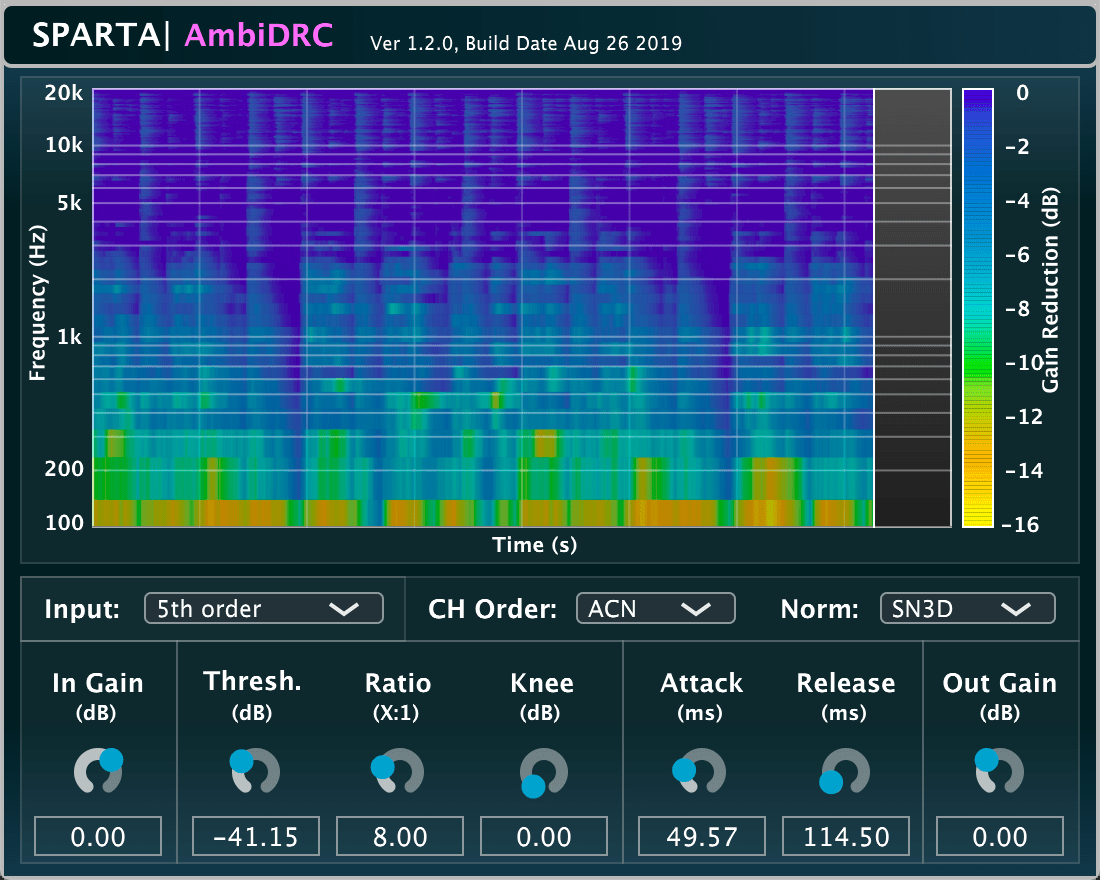
The AmbiDRC plug-in is based on the design proposed in this publication.

A frequency-dependent Ambisonic dynamic range compressor (DRC). The gain factors are derived by analysing the omnidirectional component for each frequency band, which are then applied also to the higher-order components. The spatial properties of the original signals remains unchanged; although, your perception of them after decoding may change. The implementation also keeps track of the frequency-dependent gain factors for the omnidirectional component over time, which is then plotted on the user interface for visual feedback.

This plug-in was developed by Leo McCormack.

SPARTA | AmbiENC

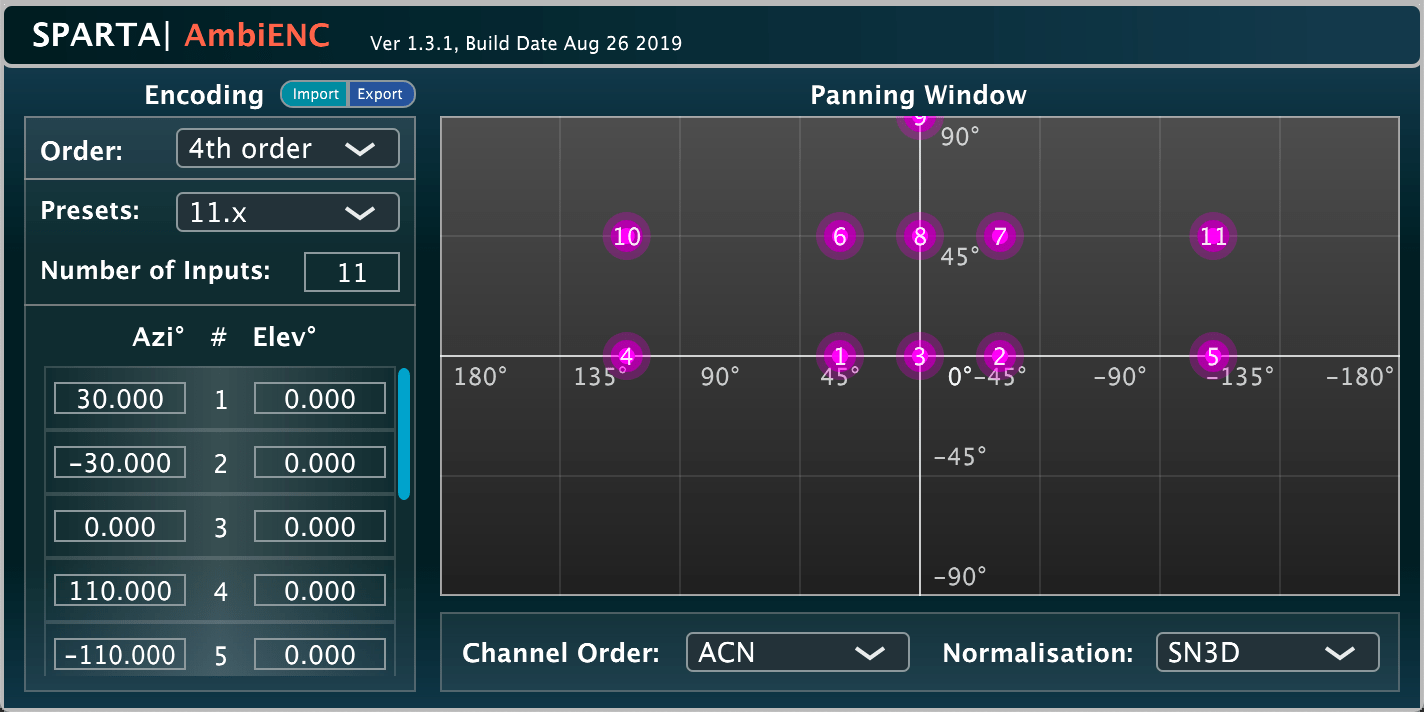
A bare-bones Ambisonic encoder which takes input signals (up to 64 channels) and encodes them into Ambisonic signals at specified directions. Essentially, these Ambisonic signals describe a synthetic sound-field, where the spatial resolution of this encoding is determined by the transform order. Several presets have been included for convenience (which allow for 22.x etc. audio to be encoded into 1-7th order Ambisonics, for example). The panning window is also fully mouse driven, and uses an equirectangular respresentation of the sphere to depict the azimuth and elevation angles of each source.

This plug-in was developed by Leo McCormack.

SPARTA | AmbiRoomSim

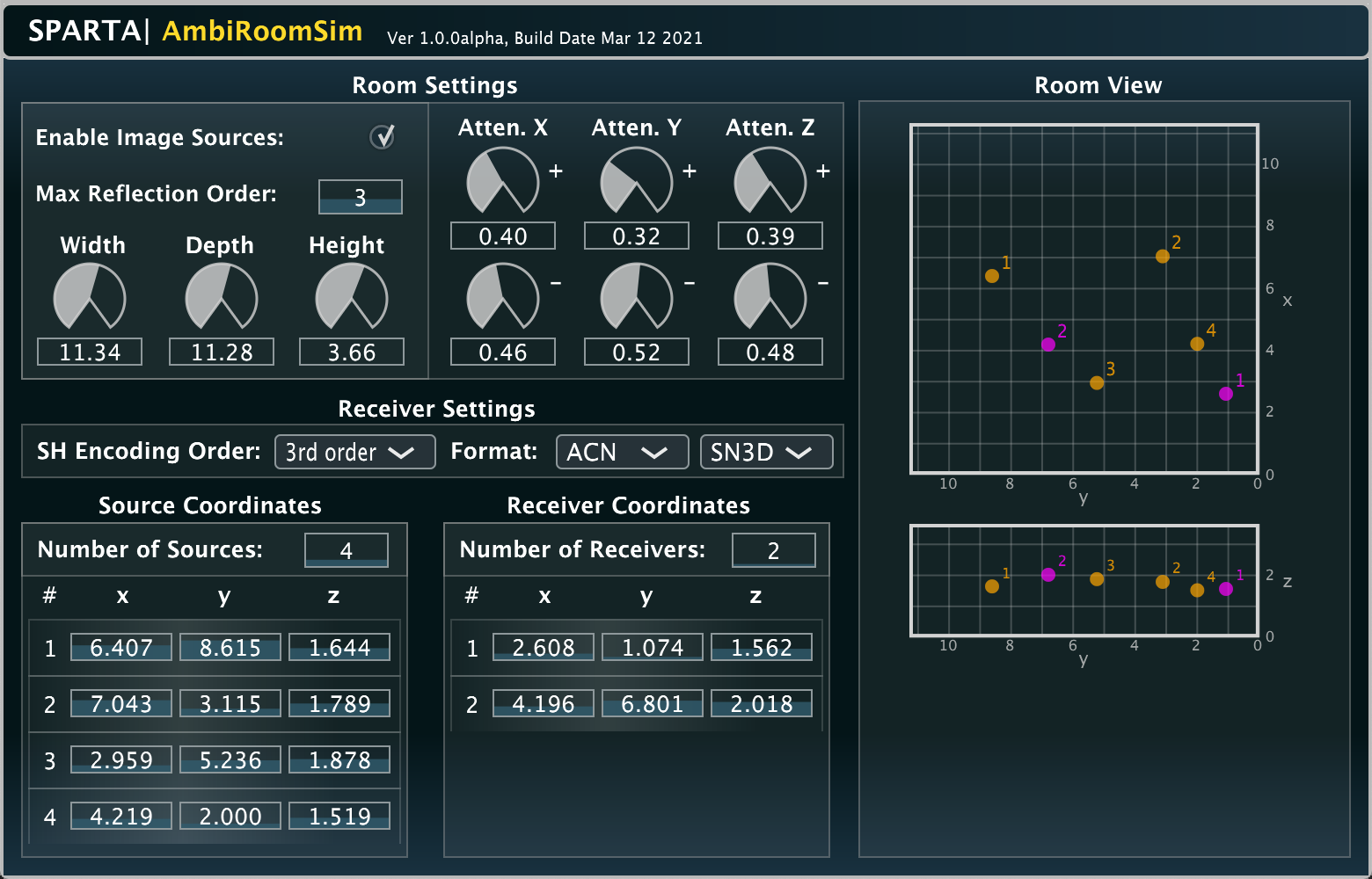
An Ambisonic room encoder that includes room reflections. It is based on the image source method using a shoebox room model. It permits multiple sources, and also multiple Ambisonic receivers up to 64 channels in total; e.g. 16x first-order or 4x third-order receivers, or 1x 7th order receiver. The output receiver channels are stacked, e.g. 1-4 channels are for the 1st first-order receiver, 5-8 for the second etc.

This plug-in was developed by Leo McCormack.

SPARTA | Array2SH

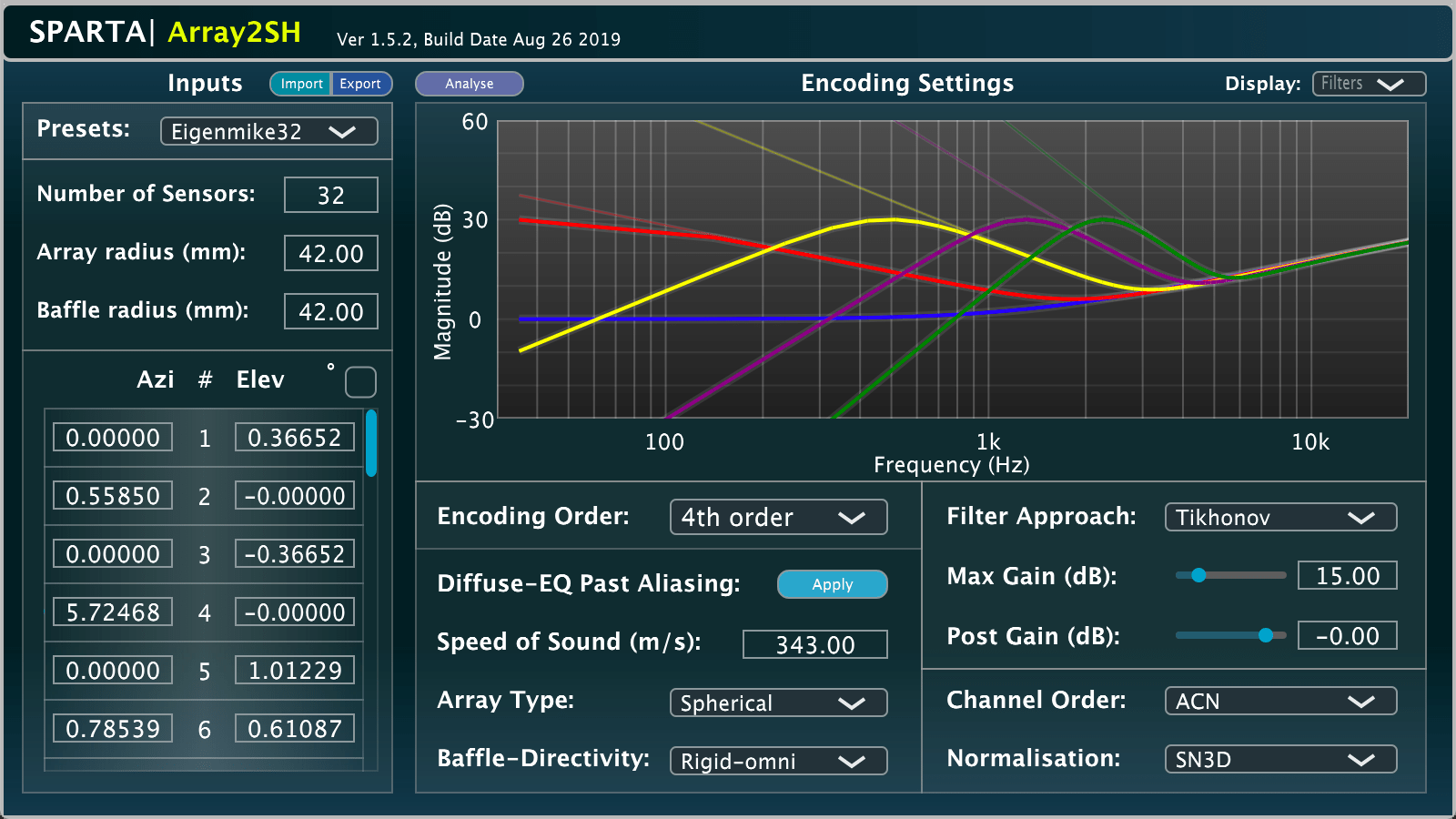
The Array2SH plug-in is related to this publication.

'Array2SH' spatially encodes spherical/cylindrical array signals into spherical harmonic signals (aka: Ambisonic or B-Format signals). The plug-in utilises analytical descriptors, which ascertain the frequency and order-dependent influence that the physical properties of the array have on the plane-waves arriving at its surface. The plug-in allows the user to specify: the array type (spherical or cylindrical), whether the array has an open or rigid enclosure, the radius of the array, the radius of the sensors (in cases where they protrude out from the array), the sensor coordinates (up to 64 channels), sensor directivity (omni-dipole-cardioid), the speed of sound, and the acoustical admittance of the array material (in the case of rigid arrays). The plug-in then determines the order-dependent equalisation curves that need to be imposed onto the initial spherical harmonic signals estimate, in order to remove the influence of the array itself. However, especially for higher-orders, this generally results in a large amplification of the low frequencies (including the sensor noise at these frequencies that accompanies it); therefore, four different regularisation approaches have been integrated into the plug-in, which allow the user to make a compromise between noise amplification and transform accuracy. These target and regularised equalisation curves are depicted on the user interface to provide visual feedback.

The plug-in also allows the user to 'Analyse' the spatial encoding performance using objective measures described in [8,10], namely: the spatial correlation and the level difference. Here, the encoding matrices are applied to a simulated array, which is described by multichannel transfer functions of plane waves for 812 points on the surface of the spherical/cylindrical array. The resulting encoded array responses should ideally resemble spherical harmonic functions at the grid points. The spatial correlation is then derived by comparing the patterns of these responses with the patterns of ideal spherical harmonics, where '1' means they are perfect, and '0' completely uncorrelated; the spatial aliasing frequency can therefore be observed for each order, as the point where the spatial correlation tends towards 0. The level difference is then the mean level difference over all directions (diffuse level difference) between the ideal and simulated components. One can observe that higher permitted amplification limits [Max Gain (dB)] will result in noisier signals; however, this will also result in a wider frequency range of useful spherical harmonic components at each order. This analysis is primarily based on code written for publication [10], which compared the performance of various regularisation approaches of encoding filters, based on both theoretical and measured array responses.

Note that this ability to balance the noise amplification with the accuracy of the spatial encoding (to better suit a given application) is very important, for example: the perceived fidelity of Ambisonic decoded audio can be rather poor if the noise amplification is set too high; therefore, typically a much lower amplification regularisation limit is used in Ambisonics reproduction when compared to sound-field visualisation algorithms, or beamformers that employ appropriate post-filtering.

For convenience, the specifications for several commercially available microphone arrays have been integrated as presets; including: MH Acoustic's Eigenmike, the Zylia array, and various A-format microphone arrays. Additionally, by releasing this plug-in, one now has the ability to build/3-D print thier own spherical and cylindrical array, while having a convenient means of obtaining the corresponing spherical harmonic siganls; for example, a four capsule open-body hydrophone array was presented in [9], which utilised this Array2SH plug-in as the first step in visualising and auralising an underwater sound scene in real-time.

This plug-in was developed by Leo McCormack, Symeon Delikaris-Manias and Archontis Politis.

SPARTA | Beamformer

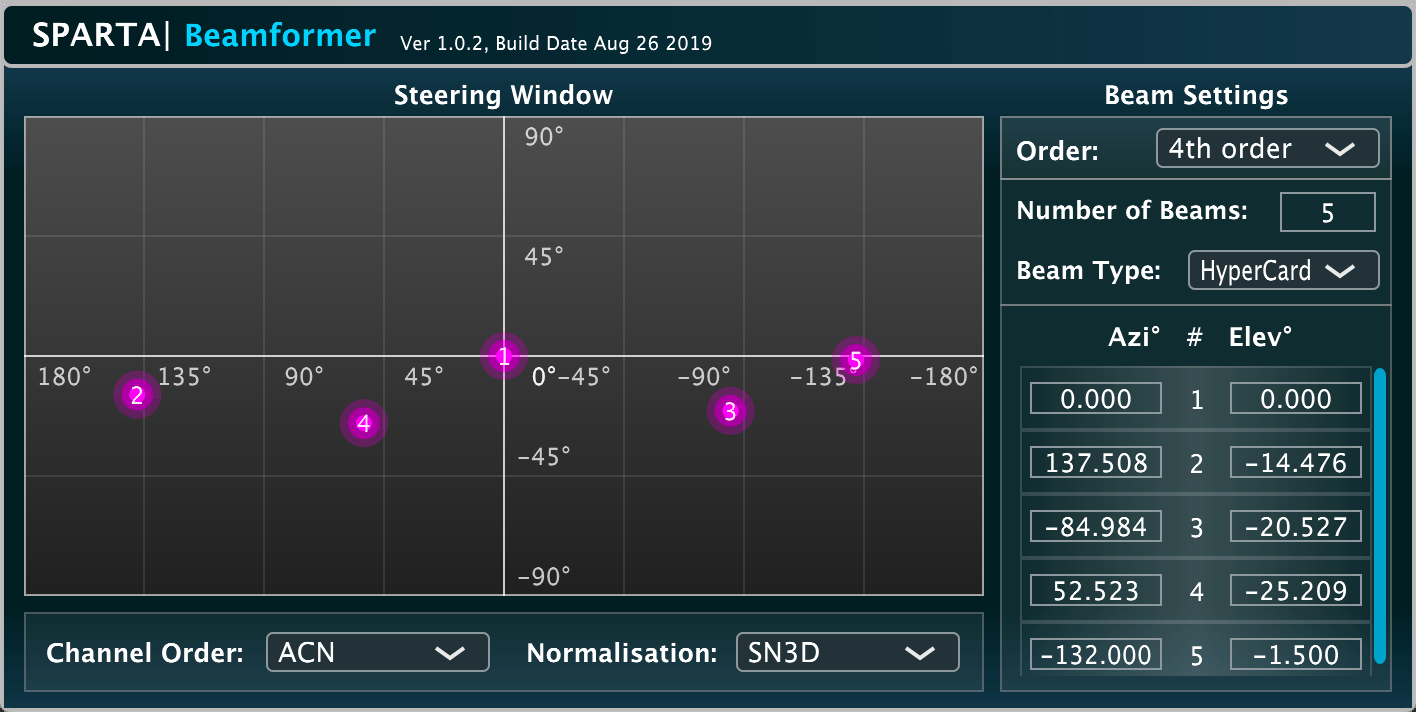
A simple beamforming plug-in. Currently includes static beam patterns only (cardioid, hyper-cardioid or max_rE weighted hyper-cardioid). More pattern options to follow in future.

This plug-in was developed by Leo McCormack.

SPARTA | Binauraliser

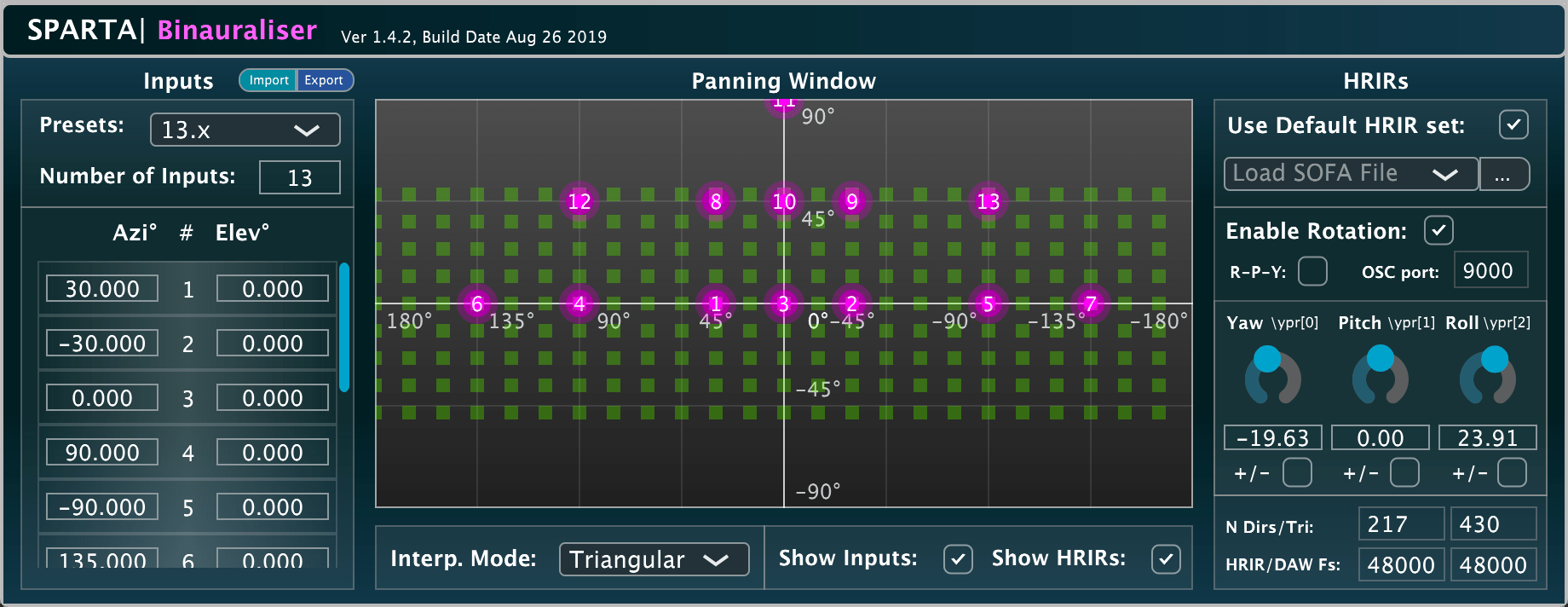
A plug-in which convolves input audio (up to 64 channels) with interpolated HRTFs in the time-frequency domain. The HRTFs are interpolated by applying amplitude-normalised VBAP gains [4] to the HRTF magnitude responses and the estimated inter-aural time differences (ITDs) individually, before being re-combined. The plug-in also allows the user to specify an external SOFA file for the convolution. Presets for popular 2D and 3D formats are included for convenience; however, the directions for up to 64 channels can be independently controlled. Head-tracking is also supported via OSC messages in the same manner as with the Rotator plug-in.

Please note that this plug-in is only suitable for HRTF-based convolution.

This plug-in was developed by Leo McCormack and Archontis Politis.

SPARTA | Decorrelator

A simple multi-channel signal decorrelator (up to 64 channels) based on randomised time-frequency delays and cascaded all-pass filters.

This plug-in was developed by Leo McCormack.

SPARTA | DirASS

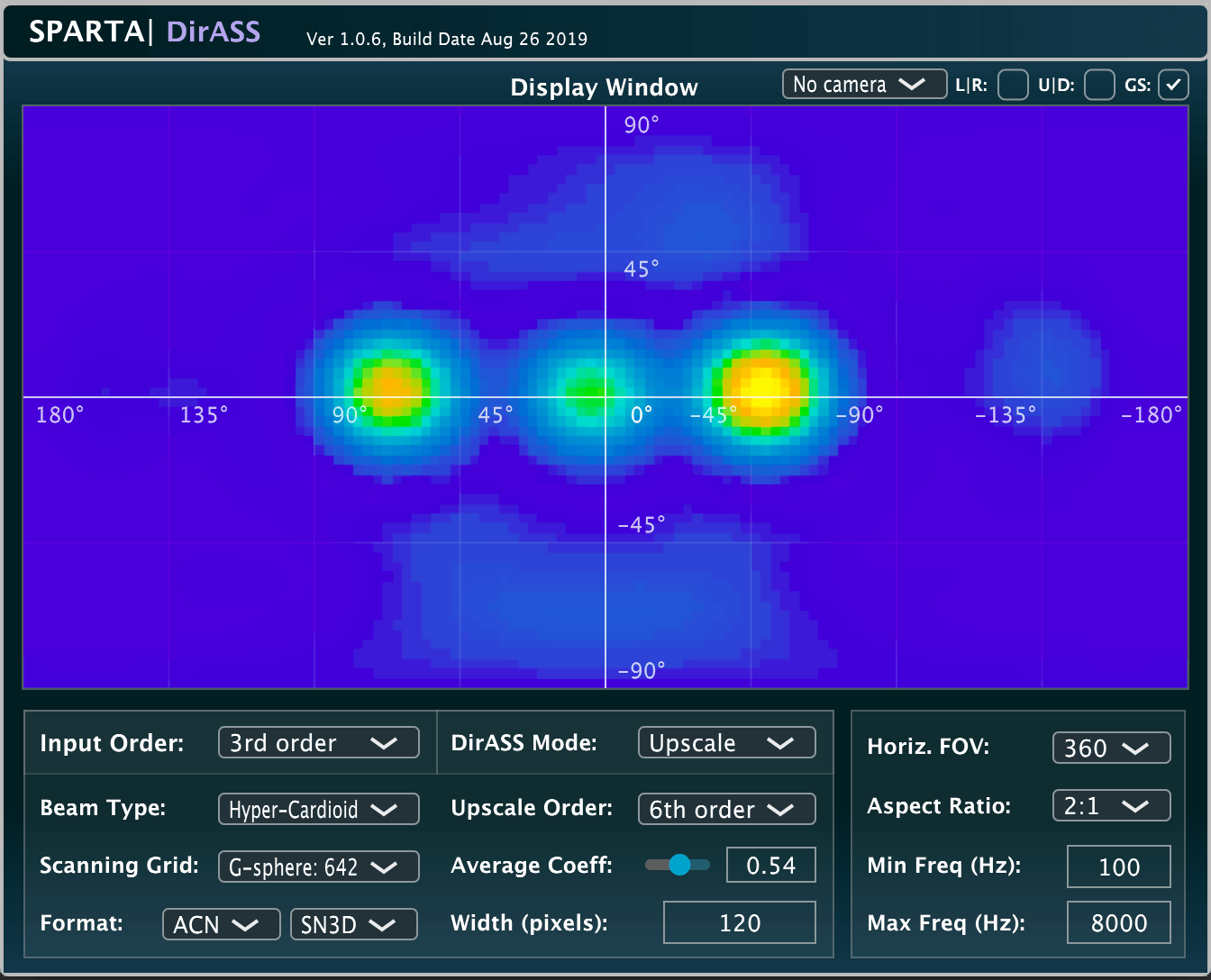
The DirASS plug-in is related to these publications: Link1, Link2.

A sound-field visualiser, which is based on the directional re-assignment of beamformer energy. This energy re-assignment is based on local DoA estimates for each scanning direction, and may be quantised to the nearest direction or upscaled to a higher-order than the input; resulting in sharper activity-maps. For example, a second-order input may be displayed with (up to) 20th order output resolution. The plug-in also allows the user to place real-time video footage behind the activity-map, in order to create a make-shift acoustic camera.

This plug-in was developed by Leo McCormack and Archontis Politis.

SPARTA | MatrixConv

A simple matrix convolver with an (optional) partitioned-convolution mode. The matrix of filters should be concatenated for each output channel and loaded as a .wav file. You need only inform the plug-in of the number if input channels, and it will take care of the rest.

• Example 1, spatial reverberation: if you have a B-Format/Ambisonic room impulse response (RIR), you may convolve it with a monophonic input signal and the output will exhibit (much of) the spatial characteristics of the measured room. Simply load this Ambisonic RIR into the plug-in and set the number of input channels to 1. You may then decode the resulting Ambisonic output to your loudspeaker array (e.g. using SPARTA|AmbiDEC) or to headphones (e.g. using SPARTA|AmbiBIN). However, please note that the limitations of lower-order Ambisonics for signals (namely, colouration and poor spatial accuracy) will also be present with lower-order Ambisonic RIRs; at least, when applied in this manner. Consider referring to Example 3, for a more spatially accurate method of reproducing the spatial characteristics of rooms, which are captured as B-Format/Ambisonic RIRs.
• Example 2, microphone array to Ambisonics encoding: if you have a matrix of filters to go from an Eigenmike (32 channel) recording to 4th order Ambisonics (25 channel), then the plugin requires a 25-channel wav file to be loaded, and the number of input channels to be set to 32. In this case: the first 32 filters will map the input to the first output channel, filters 33-64 will map the input to the second output channel, ... , and the last 32 filters will map the input to the 25th output channel. An example of such an encoding matrix may be downloaded from here. Note that these example filters employ the ACN/N3D convention, Tikhonov regularisation, and 15dB of maximum gain amplification; using the Matlab scripts from here. This should be the same as SPARTA|Array2SH when it is set to the Eigenmike preset and default settings (except N3D not SN3D).
• Example 3, more advanced spatial reverberation: if you have a monophonic recording of a trumpet and you wish to reproduce it as if it were in your favourite concert hall, first measure a B-Format/Ambisonic room impulse response (RIR) of the hall, and then convert this Ambisonic RIR to your loudspeaker set-up using HO-SIRR. Then load the resulting rendered loudspeaker array RIR into the plug-in and set the number of input channels to 1. Note that you may prefer to use HO-SIRR (which is a parametric renderer), to convert your arbitrary order B-Format/Ambisonic IRs to arbitrary loudspeaker array IRs, as the resulting output will generally be much more spatially accurate when compared to linear (non-parametric) Ambisonic decoding; as described in Example 1. For the curious reader, an example of a 12point T-design loudspeaker array IR, made using a simulation [15] of the Vienna Musikverein concert hall, may be downloaded from here. To listen to the convolved output, either arrange 12 loudspeakers in a t-design for the playback (a bit cumbersome), or use the SPARTA|Binauraliser plug-in set to "T-Design (12)" and listen over headphones.
• Example 4, virtual monitoring of a multichannel setup: if you have a set of binaural head-related impulse responses (BRIRs) which correspond to the loudspeaker directions of a measured listening room, you may use this 2 x L matrix of filters to reproduce loudspeaker mixes (L-channels) over headphones. Simply concatenate the BRIRs for each input channel into a two channel wav file and load them into the plugin, then set the number of inputs to be the number of BRIRs/loudspeakers in the mix.

This plug-in was developed by Leo McCormack and Archontis Politis.

SPARTA | MultiConv

A simple multi-channel convolver with an (optional) partitioned-convolution mode. The plugin will convolve each input channel with the respective filter up to the maximum of 64 channels/filters. The filters are loaded as a multi-channel .wav file.

Please note that this is not to be confused with the MatrixConv plug-in. For this plug-in, the number inputs = the number of filters = the number of outputs. i.e. no matrixing is applied.

• Example, headphone equalisation: post binauraliser/AmbiBIN etc., you may minimise the effect that your headphones have on the binaural output, by also convolving with (regularised) inverse filters. These filters may either be based on measurements of your own head and headphones, or you may download generic ones. For example, you can find equalisation filters for many commerically available headphones from here; which have been measured using a dummy head (more information can be found in [16]).

This plug-in was developed by Leo McCormack and Archontis Politis.

SPARTA | Panner

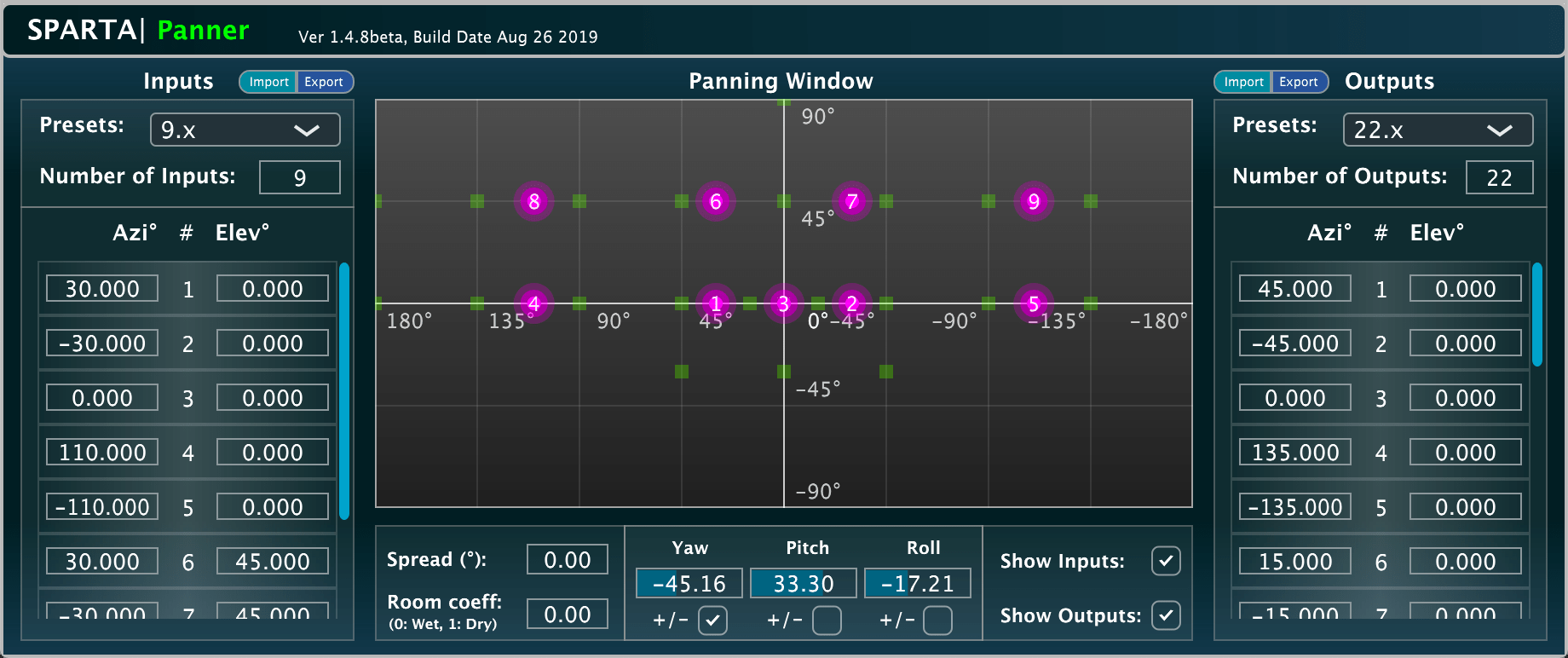
A frequency-dependent 3D panner based on the Vector-base Amplitude Panning (VBAP) method [4]. Presets for popular 2D and 3D formats are included for convenience; however, the directions for up to 64 channels can be independently controlled for both inputs and outputs; allowing, for example, 9.x input audio to be panned for a 22.2 setup. The panning is frequency-dependent to accommodate the method described in [5], which allows for more consistent loudness when sources are panned in-between the loudspeaker directions.

Set the "Room Coeff" parameter to 0 for standard power-normalisation, 0.5 for a listening room, and 1 for an anechoic chamber.

This plug-in was developed by Leo McCormack, Archontis Politis and Ville Pulkki.

SPARTA | PowerMap

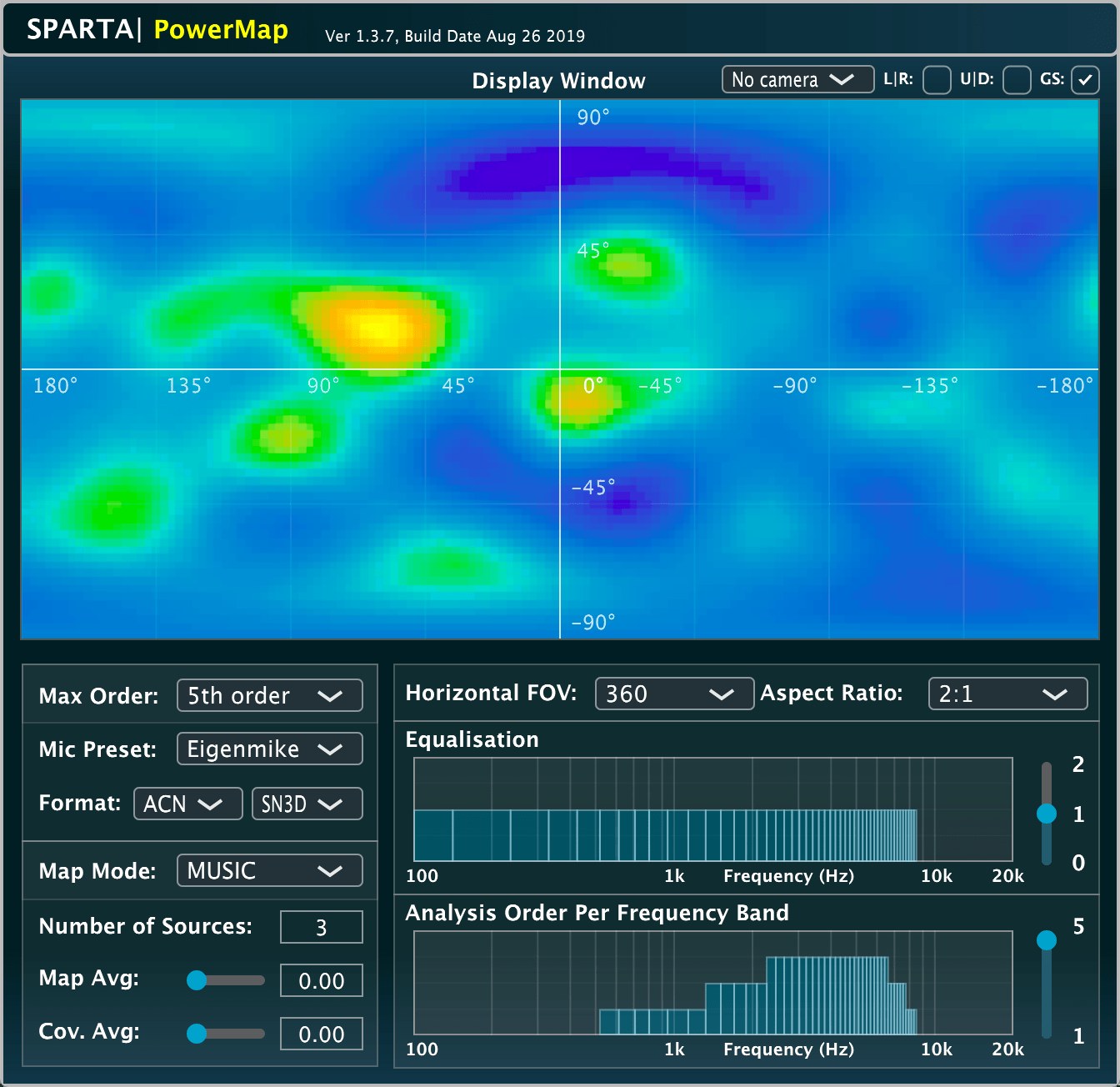
The PowerMap plug-in is a modified version of the plug-in described in this publication.

'PowerMap' is a plug-in that represents the relative sound energy, or the statistical likelihood of a source, arriving at the listening position from a particular direction, using a colour gradient; where yellow indicates high sound energy/likelihood and blue indicates low sound energy/likelihood. The plug-in integrates a variety of different approaches, including: standard Plane-Wave Decomposition (PWD) beamformer-based, Minimum-Variance Distortionless Response (MVDR) beamformer-based, Multiple Signal Classification (MUSIC) pseudo-spectrum-based, and the Cross-Pattern Coherence (CroPaC) algorithm [3]; all of which are written to operate on Ambisonic signals up to 7th order. Note that the analysis order per frequency band is entirely user definable, and presets for higher order microphone arrays have been included for convience (which provide some rough yet appropriate starting values). The plug-in utilises a 812 point uniformly-distributed spherical grid, which is then interpolated into a 2D powermap using amplitude-normalised VBAP gains (i.e. triangular interpolation). The plug-in also allows the user to place real-time video footage behind the activity-map, in order to create a make-shift acoustic camera.

This plug-in was developed by Leo McCormack and Symeon Delikaris-Manias.

SPARTA | Rotator

This plug-in applies a Ambisonic rotation matrix [6] to the input Ambisonic signals. The rotation angles can be controlled using a head tracker via OSC messages. Simply configure the headtracker to send a vector: '\ypr[3]' to OSC port 9000 (default); where \ypr[0], \ypr[1], \ypr[2] are the yaw-pitch-roll angles, respectively. The angles can also be flipped +/- in order to support a wider range of devices. The rotation order (yaw-pitch-roll (default) or roll-pitch-yaw) can also be specified. Alternatively, the rotation can be based on a Quaternion by sending vector: '\quaternion[4]'; where \quaternion[0], \quaternion[1], \quaternion[2], \quaternion[3], are the W, X, Y, Z parts of the Quaternion, respectively.

This plug-in was developed by Leo McCormack.

SPARTA | SLDoA

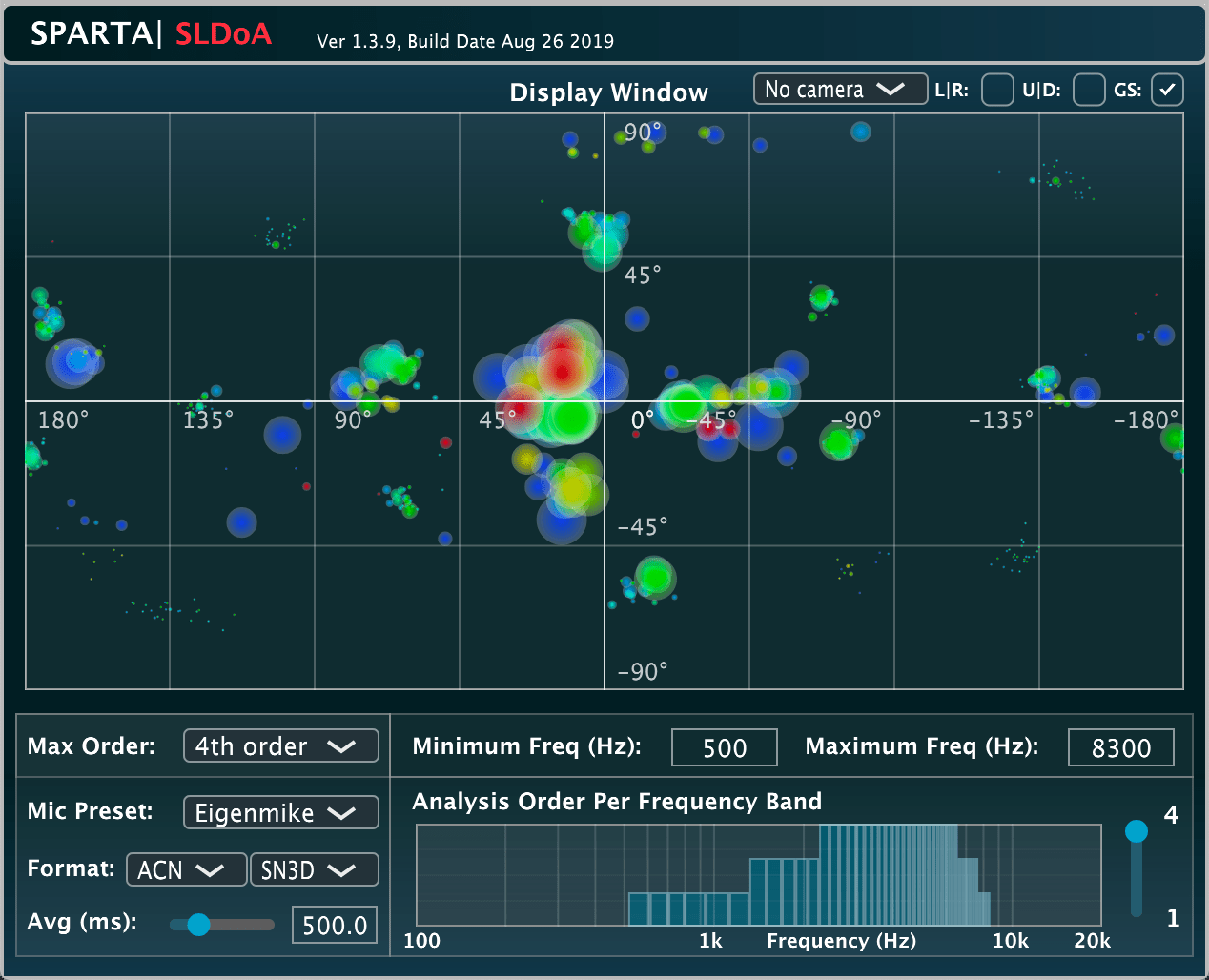
The SLDoA plug-in is related to these publications: Link1, Link2.

A spatially localised direction-of-arrival (DoA) estimator. The plug-in first uses VBAP beam patterns (for directions that are uniformly distributed on the surface of a shere) to obtain spatially-biased zeroth and first-order signals, which are subsequently used for the active-intensity vector estimation; therefore, allowing for DoA estimation in several spatially-constrained sectors for each sub-band. The low frequency estimates are then depicted with blue icons, mid-frequencies with green, and high-frequencies with red. The size of the icon and its opacity correspond to the energy of the sector, which are normalised and scaled in ascending order for each frequency band. The plug-in employs two times as many sectors as the analysis order, with the exception of the first-order analysis, which uses the traditional active-intensity approach. The analysis order per frequency band is user definable, as is the frequency range at which to analyse. This approach to sound-field visualisation/DoA estimation represents a much more computationally efficient option, when compared to the algorithms that are integrated into the 'Powermap' plug-in, for instance. The plug-in also allows the user to place real-time video footage behind the activity-map, in order to create a make-shift acoustic camera.

This plug-in was developed by Leo McCormack and Symeon Delikaris-Manias.

SPARTA | Spreader

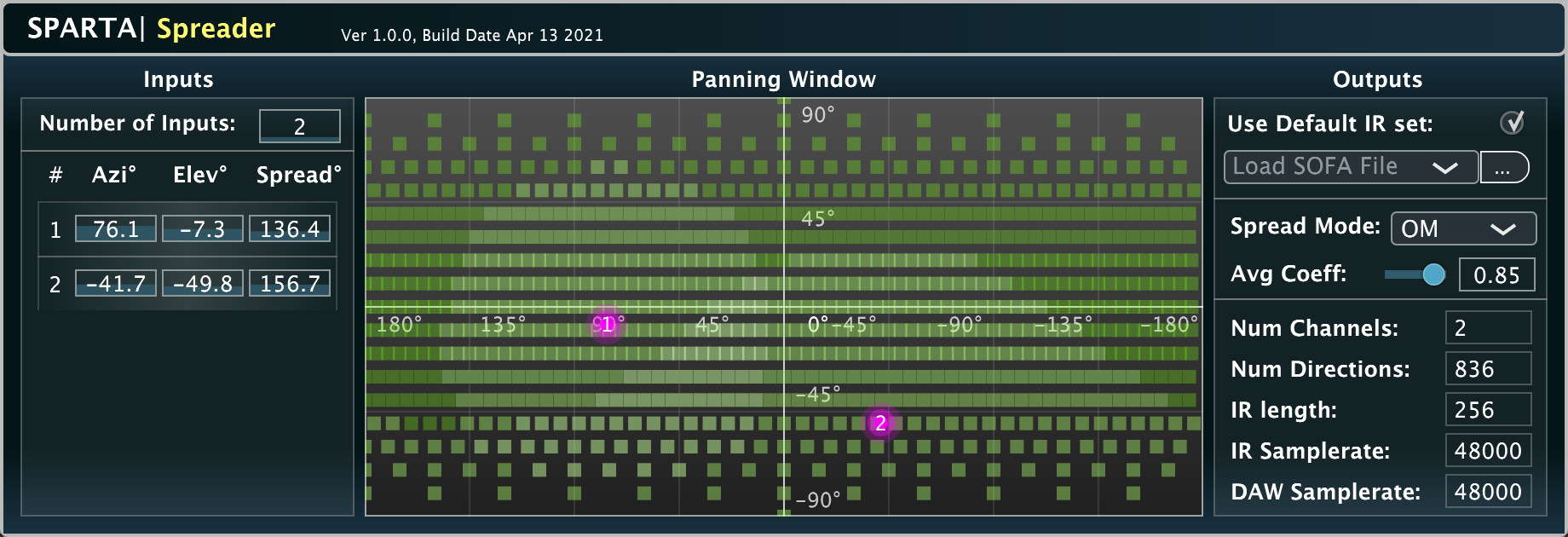
An arbitrary array (e.g., HRIRs or microphone array IRs) panner with coherent and incoherent spreading options.

This plug-in was developed by Leo McCormack and Archontis Politis.

Other plug-ins included in the SPARTA installer

COMPASS Plug-in Suite

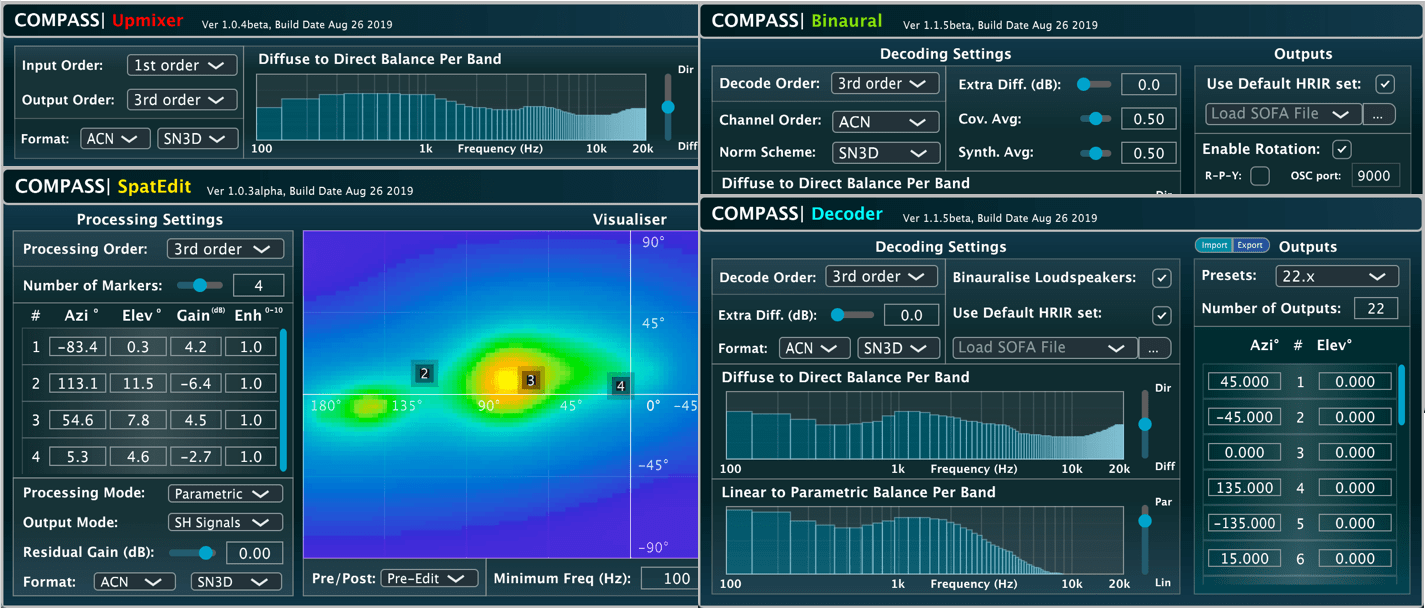
The COMPASS [13] audio plug-in suite is described in more detail here.

These plug-ins were developed by Leo McCormack and Archontis Politis.

HO-DirAC Plug-in Suite

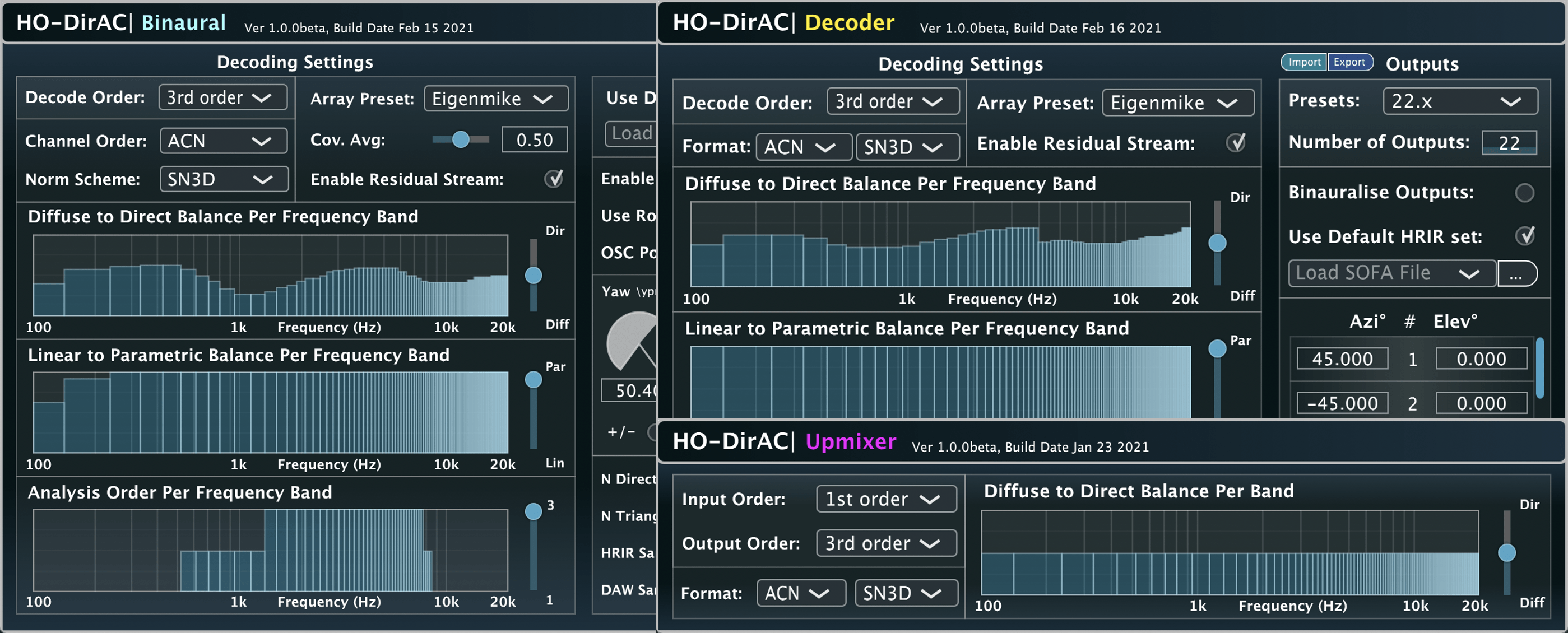
The HO-DirAC audio plug-in suite is described in more detail here.

These plug-ins were developed by Leo McCormack.

CroPaC | Binaural

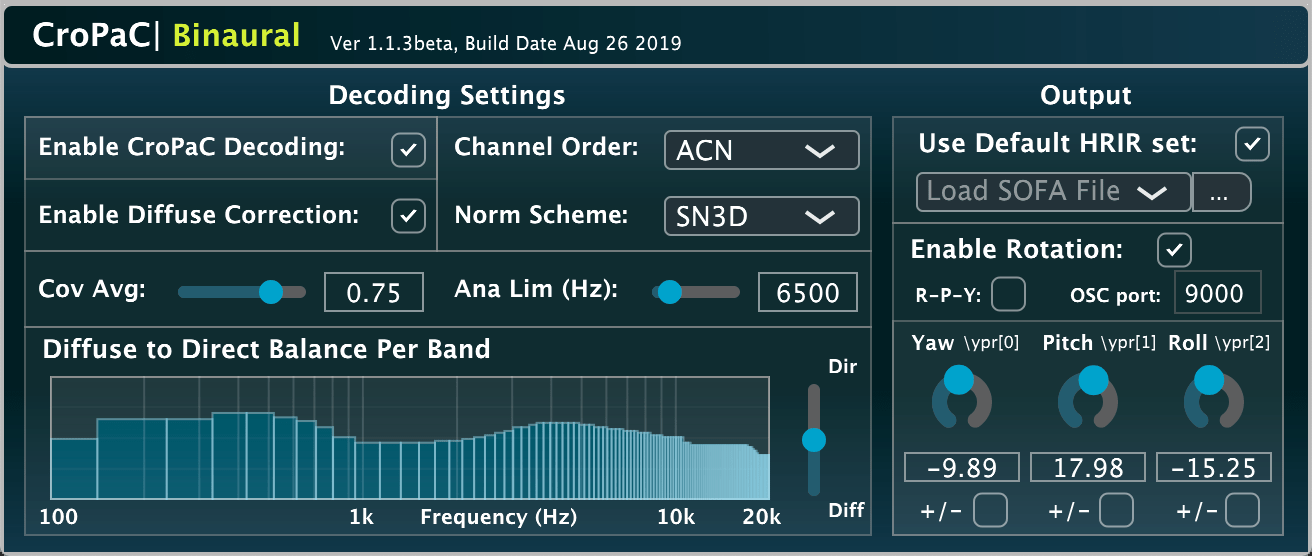
The CroPaC|Binaural plug-in is related to this publication.

A parametric first-order Ambisonic decoder for headphones [14], based on segregating the sound-field into directional and diffuse components using the Cross-Pattern Coherence (CroPaC) [3] spatial filter.

This plug-in was developed by Leo McCormack and Symeon Delikaris-Manias.

HOSIRR

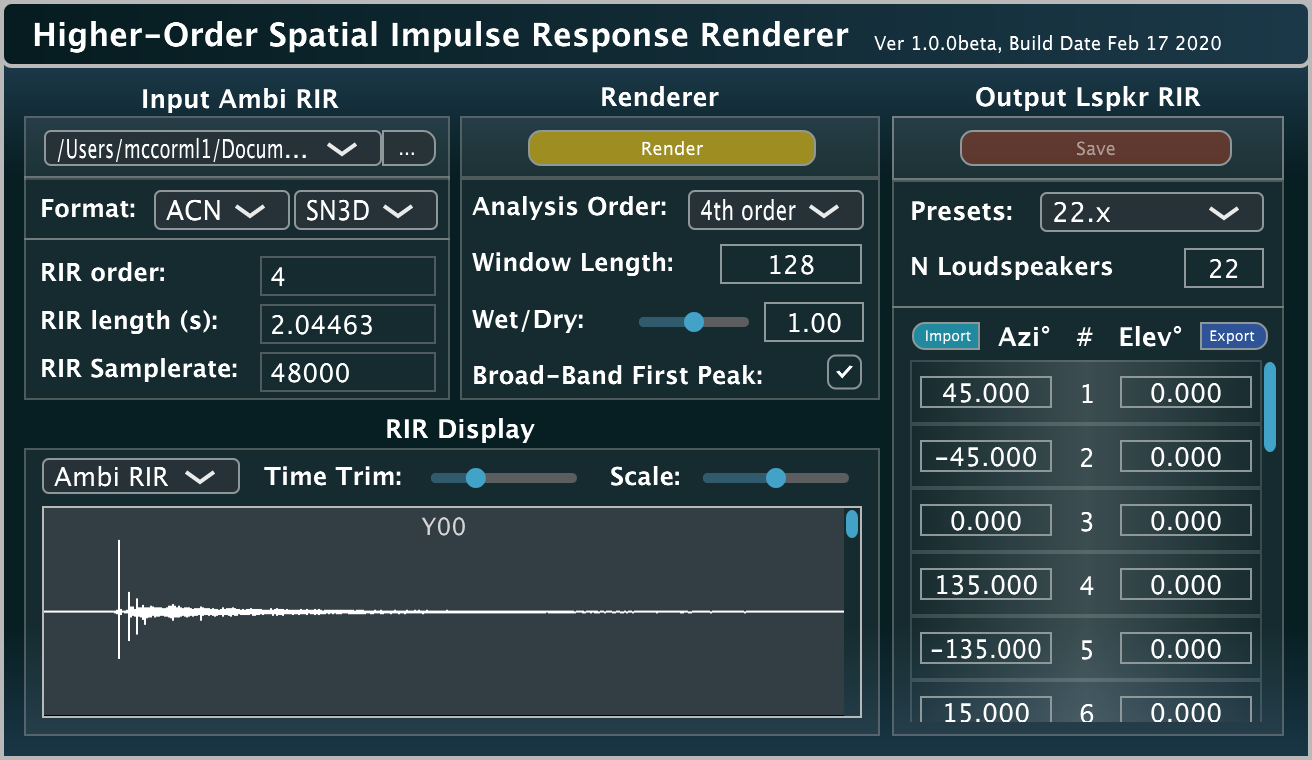
The HO-SIRR audio plug-in (and standalone App) is described in more detail here.

This plug-in/App was developed by Leo McCormack and Archontis Politis.

About the developers

• Leo McCormack: a doctoral candidate at Aalto University.
• Symeon Delikaris-Manias: post doctorate researcher at Aalto University, specialising in compact microphone array processing for DoA estimation and sound-field reproduction. His doctoral research included work on the Cross-Pattern Coherence (CroPaC) algorithm, which is a spatial post-filter optimised for high noise/reverberant environments.
• Archontis Politis: post doctorate researcher at Tampere University, specialising in spatial sound recording and reproduction, acoustic scene analysis and microphone array processing.
• Ville Pulkki: Professor at Aalto University, known for VBAP, SIRR, DirAC and eccentric behaviour.
• Christoph Hold: a doctoral candidate at Aalto University.

References

[1] Zotter, F., Frank, M. (2012). All-Round Ambisonic Panning and Decoding.
Journal of the Audio Engineering Society, 60(10), 807-820.

[2] Zotter, F., Pomberger, H., Noisternig, M. (2012). Energy-Preserving Ambisonic Decoding.
Acta Acustica United with Acustica, 98(1), 37-47.

[3] Delikaris-Manias, S., Pulkki, V. (2013). Cross pattern coherence algorithm for spatial filtering applications utilizing microphone arrays.
IEEE Transactions on Audio, Speech, and Language Processing, 21(11), 2356-2367.

[4] Pulkki, V. (1997). Virtual Sound Source Positioning Using Vector Base Amplitude Panning.
Journal of the Audio Engineering Society, 45(6), 456-466.

[5] Laitinen, M., Vilkamo, J., Jussila, K., Politis, A., Pulkki, V. (2014). Gain normalization in amplitude panning as a function of frequency and room reverberance.
55th International Conference of the AES. Helsinki, Finland.

[6] Ivanic, J., Ruedenberg, K. (1998). Rotation Matrices for Real Spherical Harmonics. Direct Determination by Recursion Page: Additions and Corrections.
Journal of Physical Chemistry A, 102(45), 9099?9100.

[7] Faller, C. (2006). Multiple-loudspeaker playback of stereo signals.
Journal of the Audio Engineering Society, 54(11), 1051-1064.

[8] Moreau, S., Daniel, J., Bertet, S. (2006). 3D sound field recording with higher order ambisonics-objective measurements and validation of spherical microphone.
in Audio Engineering Society Convention 120, Audio Engineering Society

[9] Delikaris-Manias, S., McCormack, L., Huhtakallio, I., and Pulkki, V. (2018) Real-time underwater spatial audio: a feasibility study.
in Audio Engineering Society Convention 144, Audio Engineering Society.

[10] Politis, A., Gamper, H. (2017). Comparing Modelled And Measurement-Based Spherical Harmonic Encoding Filters For Spherical Microphone Arrays.
In IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (WASPAA).

[11] Zaunschirm, M., Schörkhuber, C., and Höldrich, R. (2018). Binaural rendering of Ambisonic signals by head-related impulse response time alignment and a diffuseness constraint.
The Journal of the Acoustical Society of America, 143(6), 3616-3627.

[12] Schörkhuber, C., Zaunschirm, M., and Höldrich, R. (2018). Binaural Rendering of Ambisonic Signals via Magnitude Least Squares.
In Proceedings of the DAGA (Vol. 44).

[13] Politis, A., Tervo S., and Pulkki, V. (2018) COMPASS: Coding and Multidirectional Parameterization of Ambisonic Sound Scenes.
IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP).

[14] McCormack, L., and Delikaris-Manias, S. (2019) Parametric First-order Ambisonic Decoding for Headphones Utilising the Cross-Pattern Coherence Algorithm
In Proceedings of the 1st EAA Spatial Audio Signal Processing Symposium, Paris, France, September 6-7th 2019.

[15] Favrot, S. and Buchholz, J.M., (2019). "LoRA: A loudspeaker-based room auralization system".
Acta Acustica united with Acustica, 96(2), pp.364-375.

[16] Bernschutz, B., (2013). A spherical far field HRIR/HRTF compilation of the Neumann KU 100.
In Proceedings of the 40th Italian (AIA) annual conference on acoustics and the 39th German annual conference on acoustics (DAGA) conference on acoustics (p. 29). AIA/DAGA.